Estudiaremos únicamente las posiciones relativas
a partir de las ecuaciones generales (o implícitas)
Posiciones
de dos planos: 
Para el sistema formado por ambas ecuaciones,  ,
caben las siguientes posibilidades:
,
caben las siguientes posibilidades:
 .
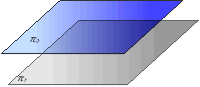
Entonces los planos coinciden (fig. 1)
.
Entonces los planos coinciden (fig. 1) .
Entonces son planos paralelos, y distintos (fig. 2)
.
Entonces son planos paralelos, y distintos (fig. 2)
- En cualquier otro caso, el rango del sistema es
2, y entonces los planos definen una recta (fig. 3)


Posiciones
de dos rectas:

Llamaremos A a la matriz del sistema formado por esas cuatro ecuaciones, y A’ a la ampliada.
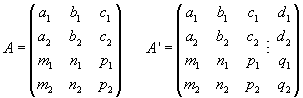
Éstas son las posibilidades:
- rang(A) = 2, rang(A’)=2. Entonces, son dos rectas
coincidentes.
- rang(A) = 2, rang(A’)=3. Entonces, son dos rectas
paralelas, distintas.
- rang(A) = 3, rang(A’)=3. Entonces, son dos rectas
secantes; su punto de corte es la solución del sistema.
- rang(A’)=4, es decir, Det(A’) ¹
0. Entonces, se dice que las rectas
se cruzan.
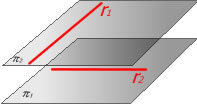
Dos rectas que se cruzan siempre podrán situarse
en dos planos paralelos. Además, éste es el único caso en el que no existe un
plano que contenga las dos rectas (rectas no
coplanarias)
Posiciones
de recta y plano:
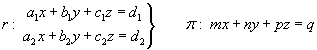
Llamaremos A a la matriz del sistema formado por esas tres ecuaciones, y A’ a la ampliada.
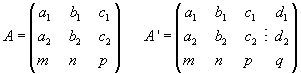
Éstas son las posibilidades:
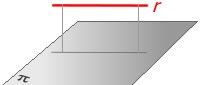
- rang(A) = 2, rang(A’)=2. Entonces, la recta está
contenida en el plano (fig. 1).
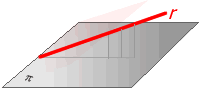
- rang(A) = 2, rang(A’)=3. Entonces, la recta es paralela
al plano, y no contenida en él (fig. 2).
- rang(A) = 3, rang(A’)=3. Entonces, se dice que la recta es secante al plano.
El punto de corte es la solución del sistema (fig. 3)

Es importante darse cuenta de que el paralelismo
de recta y plano se da exactamente cuando Det(A) = 0.
Posiciones
de 3 planos: 
Llamaremos A a la matriz del sistema formado por esas tres ecuaciones, y A’ a la ampliada.
Éstas son las posibilidades:
- rang(A) = 1, rang(A’)=1. Entonces, los 3 planos
coinciden.
- rang(A) = 1, rang(A’)=2. Entonces, son 3 planos
paralelos (Dos de ellos pueden coincidir.)
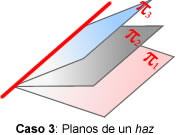
- rang(A) = 2, rang(A’)=2. Entonces, los 3 planos
contienen una misma recta (planos de un haz)
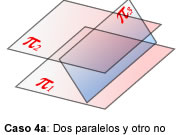
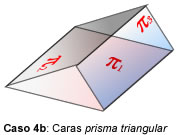
- rang(A) = 2, rang(A’)=3. Entonces, hay dos posibilidades:
a) Hay 2 planos paralelos, y el otro los
corta b) Los tres son caras de un prisma
triangular
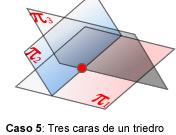
- rang(A) = 3, rang(A’)=3. Entonces, los planos
tienen exact.un punto común (caras de triedro)
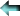
 ,
caben las siguientes posibilidades:
,
caben las siguientes posibilidades:



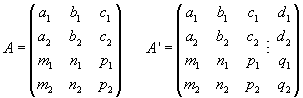

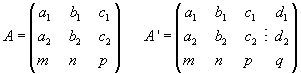
![]()


![]()



