|
ACTIVIDAD 3.2 |
|||
|
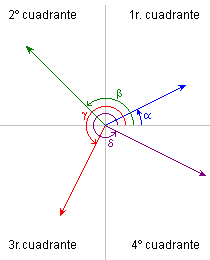
En la figura tienes cuatro vectores con argumentos respectivos a, b, g y d. Los argumentos se suelen expresar
en grados o en radianes; nosotros lo haremos en grados. Observa
que, dado un vector: Se consideran positivos los ángulos recorridos a partir de OX en sentido contrario a las agujas del reloj, y negativos los recorridos en el mismo sentido. Multiplicidad de argumentos. Un mismo vector tiene infinidad de argumentos: si a es el argumento comprendido entre 0º y 360º, los demás difieren de él en una o varias vueltas de circunferencia, es decir, en 360º o en un múltiplo, positivo o negativo, de 360º. Así pues, 30º, 390º, 750º, -330º, ... pueden ser argumentos de un mismo vector. |
 |
,
que podemos considerar con origen en el origen de coordenadas, como
el ángulo que forma con el semieje de las abscisas positivas
OX.|
ACTIVIDAD INTERACTIVA Este vector tiene módulo 3,5, que no puedes variar, y argumento 121,5º, que sí que puedes variar moviendo el punto verde. 1) Construye vectores con módulo 3,5 y con argumentos
de:
2) ¿Dónde están situados los extremos de todos los vectores que tienen por módulo 3,5 si los dibujamos todos con el mismo origen? SOLUCIÓN |
|
| PROPUESTA DE TRABAJO |
a) Dibuja en un mismo plano cuatro vectores con módulo 4 cm y con argumentos 30º, 135º, 210º y 330º.
b) Dibuja en otro plano cuatro vectores con módulo 2,5 cm y con argumentos 90º, 1260º, - 450º y 630º.
c) Dibuja en un tercer plano cuatro vectores con módulo 3 cm y con argumentos 45º, 120º, 225º y 300º.
|
FIN DE LA ACTIVIDAD 3.2 |
|||