|
|
- Taula creuada entre els notes de dues assignatures.
Per als 100 alumnes de primer cicle d'ESO d'un institut s'ha fet un
estudi de les qualificacions de matemàtiques i de llengua. Les
dades se'ns han donat així:
Superen les dues matèries: 64.
No han superat les matemàtiques: 30.
No han superat la llengua: 27.
Creieu que les dades són coherents? En cas afirmatiu, doneu-les
mitjançant una taula de doble entrada i estudieu l'afirmació
"Hi ha molta relació entre les notes de les dues àrees".
- Relació entre la variable SEXE i la variable
TORN en BAT2.XLS.
Aprofiteu les taules dinàmiques i
les diverses opcions per estudiar l'assistència al nocturn per sexes,
a partir de les dades del fitxer BAT2.XLS, amb el qual ja heu
treballat. Contesteu les preguntes següents:
- Quina variable heu posat a les files i quina a les columnes de
la taula creuada?
- Quin percentatge dels alumnes del nocturn són noies? Per
contestar la pregunta anterior, heu fet servir percentatges per
files o percentatges per columnes?
- Quin percentatge de noies va al nocturn? Per contestar la pregunta
anterior, heu fet servir percentatges per files o percentatges per
columnes?
- Quina és la mitjana de convocatòries de 2n de batxillerat
que correspon a les noies del nocturn? Per què?
- Correlacions lineals.
Si es calculés les correlacions entre els parells de variables
que s'indiquen seguidament, es trobarien coeficients de correlació
lineal de valor absolut gran. Indiqueu en cada cas si el coeficient
resultant seria positiu o negatiu i si, realment, es pot parlar de relació
entre les variables indicades o bé si cal considerar la influència
d'una tercera variable.
- En una població escolar d'alumnes dels tres darrers anys
de primària, resultats d'un test sobre habilitat per la lectura
i nombre del calçat.
- En la població d'una ciutat, nombre de casos de grip i
nombre de gelats venuts durant una setmana.
- A Espanya, en un determinat període de deu anys, el nombre
de divorcis oficialitzats cada any (1986,
19.487; 1987, 21.126; 1988, 22.449; 1989, 23.063; 1990, 23.191;
1991, 26.224; 1992, 26.783; 1993, 28.854; 1994, 32.522; 1995, 33.104;
dades que, com podeu veure, van anar augmentant) i el valor
del producte nacional brut (feu suposicions
sobre aquesta dada, que amb l'objectiu que té l'exercici
tampoc no cal que siguin gaire acurades.)
- Pressupost dels equips de futbol de la Primera Divisió
i classificació que obtenen.
- Dels gràfics següents, digueu quin correspon a una
correlació lineal de 0,25, quin a una correlació lineal
de –0,56, quin a una correlació lineal de –0,74
i, finalment, quin a una correlació lineal de 0,92.
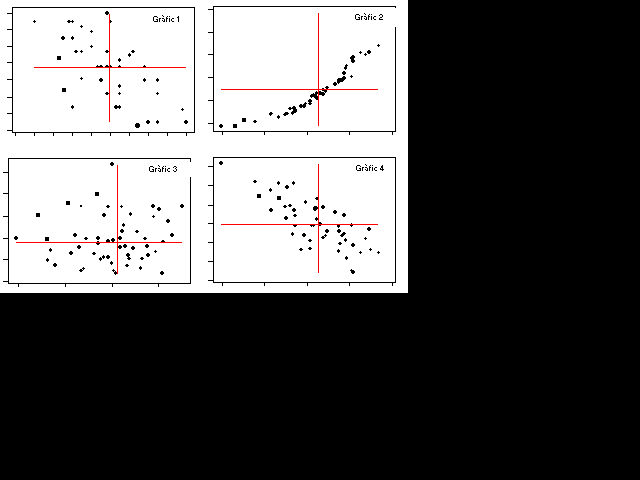
- Estudi de la correlació entre la nota
de l'examen de selectivitat i la de l'expedient.
Calculeu, per als alumnes del fitxer PAU.XLS, quina és
la correlació lineal entre la nota de l'expedient escolar (variable
EXP) i la nota de l'examen (variable PROVA, calculada en una pràctica
anterior). Suposant que l'any següent el comportament del conjunt
de l'alumnat serà el mateix, calculeu tal com es mostra a la
pràctica 4, quina nota es pot estimar
que trauria un alumne que té un 6,25 de la variable EXP.
- (Opcional) Redacteu un comentari sobre les reflexions
de caràcter conceptual/didàctic que heu pogut anotar en el desenvolupament
de les activitats dirigides proposades en el context de la pràctica
6 d'aquest mòdul. En el comentari incloureu alguns dels resultats numèrics
a què heu arribat i que us han ajudat a arribar a les conclusions que
comenteu.
- (Opcional) Correlació entre les monedes d'euro.
En aquest exercici continuem l'estudi sobre els bitllets i treballem
amb les dades les monedes d'euro, que es descriuen a la taula següent.
| Valor en
€ |
Diàmetre (mm) |
Gruix (mm) |
Pes (g) |
Color |
| 2 |
25,75 |
2,20 |
8,5 |
blanc/groc |
| 1 |
23,25 |
2,33 |
7,5 |
groc/blanc |
| 0,5 |
24,25 |
2,38 |
7,8 |
groc |
| 0,2 |
22,25 |
2,14 |
5,74 |
groc |
| 0,1 |
19,75 |
1,93 |
4,1 |
groc |
| 0,05 |
21,25 |
1,67 |
3,92 |
vermellós |
| 0,02 |
18,75 |
1,67 |
3,06 |
vermellós |
| 0,01 |
16,25 |
1,67 |
2,3 |
vermellós |
- A les pràctiques heu pogut estimar l'ample que es donaria a un
bitllet de 300 € per ser consistents amb el disseny dels de curs
legal. Feu un estudi semblant per deduir quina seria la mesura de
l'alçària de l'hipotètic bitllet de 300 €.
Com que hi ha diverses possibilitats per fer aquest estudi (amb
tots els bitllets, traient els atípics, fent servir el resultat
de l'estimació de l'ample...), cal que expliqueu com ho heu fet.
- Feu un gràfic que mostri el diàmetre de les monedes segons el
seu valor. Cal que es faci avinent que (coincidentment amb el color)
hi ha tres categories molt diferenciades en aquest nou sistema monetari.
- Quines de les magnituds de les monedes mostren una correlació
lineal més gran?
- (Opcional) Feu una estimació de les característiques que tindria
la moneda d'1 € si estigués en el grup de les monedes grogues.
(Cal que expliqueu el procediment que heu seguit.)
- (Opcional) Una reflexió sobre la causalitat
i la casualitat amb les dades del fitxer TERCERJM.XLS.
- Calculeu el coeficient de correlació entre l'altura de
cada alumne i el nombre de germans (variables ALALUMNE i GALUMNE)
restringint el càlcul únicament als alumnes de l'EATP
codificat com a 1 (EATP d'estadística). (Heu de fer servir
filtres o ordenar dades.) Veureu que surt un valor negatiu força
alt. Vol dir això que com més germans siguin en una
família es pot deduir que seran més baixets?
- Calculeu també la correlació entre les dues variables
esmentades en tot el conjunt d'alumnes del fitxer i comenteu molt
breument el resultat.
- (Opcional) Covariància gran o petita?
Una reflexió sobre el fet que no es pot parlar de covariància
gran o covariància petita, sinó que s'ha d'observar el
coeficient de correlació lineal. Fareu servir dades del fitxer
DADES74.XLS.
Calculeu la covariància i el coeficient de correlació
lineal entre les variables ALT1 i ALT3; entre les variables ALT3 i ENV3
(envergadura o distància entre les puntes dels dits amb els braços
oberts en creu) i entre les variables ALT3, PES3. Comenteu molt breument
els resultats.
- (Opcional) A la pràctica 5 s'ha fet una estimació del pes d'una persona
a 16 anys a partir del seu pes a 14 anys i del sexe.
- Feu un estudi anàleg que us permeti fer l'estimació de l'alçària
a 16 anys d'un noi o una noia que a 14 anys tenia una alçària de
165 cm.
- Expliqueu la conclusió (tan acurada com sigui possible) i el procediment
que heu seguit per arribar-hi; si ho creieu convenient, adjunteu
algun gràfic.
- (Opcional) Com a pas previ per a la introducció
d'un nombre que ens ajudi a mesurar el grau de relació entre
dues variables, en cas de variables categòriques cadascuna de
les quals només tingui dos valors, es defineix el que s'anomena
raó creuada.
|
|
Variable B |
|
Variable A
|
Valor
B1 |
Valor
B2 |
| Valor
A1 |
f11 |
f12 |
| Valor
A2 |
f21 |
f22 |
En una taula com l'anterior, es defineix com a raó creuada
el resultat de dividir f11f22
entre f12f21.
- Comproveu que si els percentatges per files coincideixen en les
dues files (homogeneïtat en la resposta de la variable B respecte
a les categories de la variable A; una variable no influeix sobre
l'altra; de vegades es diu que hi ha independència), la raó
creuada val 1.
- Amb els exemples de l'apartat Causalitat
o casualitat? dels document de fonaments (o amb altres exemples
que us fabriqueu), raoneu intuïtivament entre quina gamma de
valors de la raó creuada diríeu que hi ha força
relació entre les variables estudiades.
|