1r Teorema fonamental del càlcul integral
Anem a visualitzar el que ens demostra el 1r Teorema fonamental del càlcul integral.
1. A la finestra tens dibuixada una funció contínua f(x) i, si voleu, també la gràfica de F(x) que és una primitiva seva a la qual hem ajustat la constant d'integració per tal que F(0)=0
2. Ara desplaça el punt P(x,0) per l'eix X i veuràs:
- Que es pinta la zona limitada per les corbes (y=f(x), Eix OX, x=0 i x=a) i es calcula la seva ÀREA.
- I que per a cada punt anem dibuixant el punt de coordenades (x, ÀREA(x)).
És a dir pintem la traça de la funció
àrea
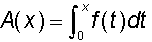
és a dir tens dibuixada la gràfica de la funció Y=A(x)
3. Observa que :
- Aquesta funció àrea és la del 1r teorema Fonamental
del Càlcul Integral
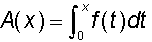
4. Ara visualitza, si encara no ho has fet, la funció F(x) i observa que:
- Els punts de gràfica de A(x) coincideixen amb els de primitiva de la f(x) és a dir F(x) que hem dibuixat prèviament.
- El requeriment que hem imposat a la primitiva de f(x) de que F(0)=0 és degut al fet que A(0)=0.
4. Conclusió:
- Acabem de visualitzar el 1r Teorema fonamental del càlcul
integral
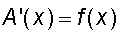o escrit en llenguatge de diferencials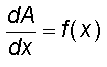 
5. Repeteix l'observació:
- Canvia la definició de f(x) per altra funció contínua.
- Prem CTRL-F (o un clic en la doble fletxa de la part superior dreta de la finestra GeoGebra) per actualitzar la imatge i esborrar la traça anterior
- Desplaça el punt P(x,0)
per l'eix i observa la traça
de la gràfica de la funció Àrea
(x)
Antoni Garrido Muñoz, 31/1/2007 (revisió del 27/1/2009), Creat amb GeoGebra