Si volem demostrar això,
algun dels factors a , b , i c haurà de portar per força
a la seva vegada els factors 2, 3 i 5 (descomposició factorial
de 30) o entre la combinació dels tres els portaran.
Partim del teorema de Pitàgoras, que aplicat a aquest triangle es
compleix:
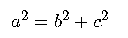 Per tant, la suma del quadrat de b i c ha de ser un quadrat
perfecte.
Analitzarem quin és l'últim dígit dels quadrats de tots els nombres
naturals (analitzant, igualment, el seu últim dígit):
Per tant, la suma del quadrat de b i c ha de ser un quadrat
perfecte.
Analitzarem quin és l'últim dígit dels quadrats de tots els nombres
naturals (analitzant, igualment, el seu últim dígit):
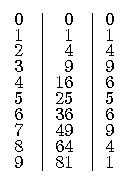 Veiem que l'últim dígit del quadrat de qualsevol nombre ha de ser:
0, 1, 9, 4, 6 o 5.
Complint el teorema de Pitàgoras, la suma d'aquests nombres
Veiem que l'últim dígit del quadrat de qualsevol nombre ha de ser:
0, 1, 9, 4, 6 o 5.
Complint el teorema de Pitàgoras, la suma d'aquests nombres
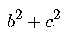 ha d'acabar en:
ha d'acabar en:
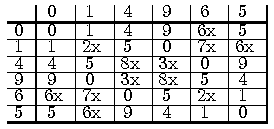 Si aquesta suma ha de ser el quadrat perfecte d'un nombre natural,
les sumes que acabin en 2, 3, 6, 7, i 8 (tenen una x al costat),
mai ho podran ser i, per tant, queden descartats.
En aquesta taula veiem que els factors 2 i 5 ja hi són inclosos.
Dígits que, o parteixen de, o són acabats en :
Si aquesta suma ha de ser el quadrat perfecte d'un nombre natural,
les sumes que acabin en 2, 3, 6, 7, i 8 (tenen una x al costat),
mai ho podran ser i, per tant, queden descartats.
En aquesta taula veiem que els factors 2 i 5 ja hi són inclosos.
Dígits que, o parteixen de, o són acabats en :
- 0 Ja porten el 2 i el 5 inclosos (són sempre múltiples de 10)
- 2 Ja porten el 2 inclòs
- 5 Ja porten el 5 inclòs
Veiem que totes les combinacions o porten elles mateixes el 2 o
el 5, o els seus antecedents els portaven i, per tant, ells ho
porten.
Ara intentarem trobar el factor 3.
Tots els números naturals accepten alguna d'aquestes 3 formes:
 Suposem que a , b, o c no portés el factor 3 directament
(no es complís abc=30, que a o b fós del tipus 3n + 1
o 3n + 2). Complint Pitàgoras:
Suposem que a , b, o c no portés el factor 3 directament
(no es complís abc=30, que a o b fós del tipus 3n + 1
o 3n + 2). Complint Pitàgoras:
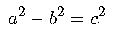 el segon catet tindria el valor de:
el segon catet tindria el valor de:
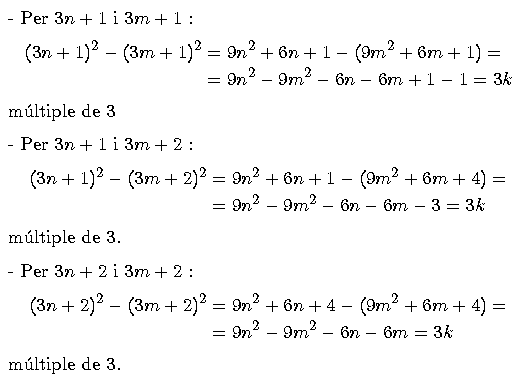 El factor 3 hi apareix sempre.
Per tant, si sempre hi ha inclòs el factor 3 (i el 2 i el 5
prèviament demostrats), l'equació abc=30n es compleix.
El factor 3 hi apareix sempre.
Per tant, si sempre hi ha inclòs el factor 3 (i el 2 i el 5
prèviament demostrats), l'equació abc=30n es compleix.
 Tornar a l'enunciat del problema
Tornar a l'enunciat del problema
 Tornar a la pàgina principal
Tornar a la pàgina principal
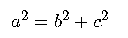
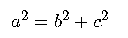

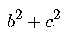


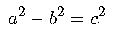
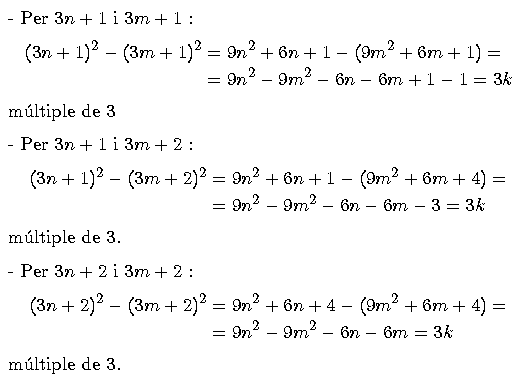
 Tornar a l'enunciat del problema
Tornar a l'enunciat del problema
 Tornar a la pàgina principal
Tornar a la pàgina principal