|
Sigui
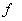 una
funció contínua en l’interval una
funció contínua en l’interval 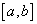 tal
que pren valors de signes diferents en els extrems tal
que pren valors de signes diferents en els extrems 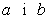 de
l’interval aleshores existeix un de
l’interval aleshores existeix un 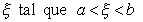 i i 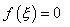
Demostració:
(no s’exigeix aquesta demostració en el currículum del Batxillerat).
Suposem
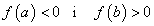
Sigui
 X
no és buit ja que X
no és buit ja que 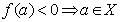
X
està acotat superiorment per b pel Teorema del suprem
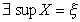
Anem
a demostrar el següent

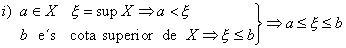
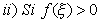 pel
Lema anterior existeix un entorn de pel
Lema anterior existeix un entorn de 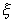 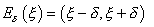
tal
que 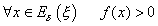 per
tant existeix per
tant existeix 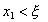 tal
que tal
que 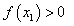 i d’aquesta
manera i d’aquesta
manera 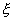 no seria
suprem del conjunt X. no seria
suprem del conjunt X.
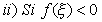 pel
Lema anterior existeix un entorn de pel
Lema anterior existeix un entorn de 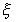 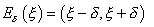
tal
que 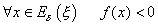 per
tant existeix per
tant existeix 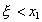 tal
que tal
que 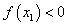 i d’aquesta
manera i d’aquesta
manera 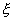 no
seria suprem del conjunt X. no
seria suprem del conjunt X.
Interpretació gràfica del teorema de Bolzano.
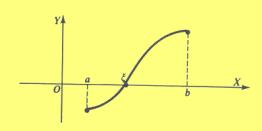
Observació:
Aquest
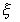 no té
perquè ser únic. no té
perquè ser únic.
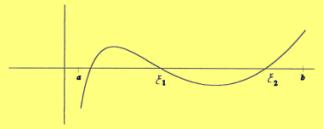
Necessitat
de les hipòtesis.
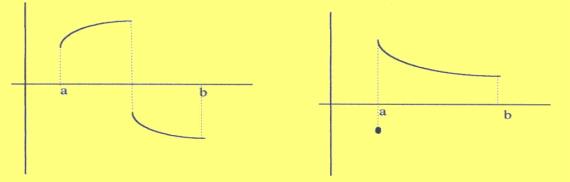
És
necessària la hipòtesis de la continuïtat de
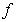 en
en 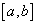 ja
que si ja
que si 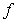 no és
contínua no té perquè existir no és
contínua no té perquè existir
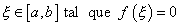
 és
suficient és
suficient 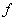 contínua
en contínua
en 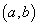
|

