ESTUDI
DE LES EQUACIONS DE SEGON GRAU
1.- Estudi de les solucions de l'equació reduïda
Si b = 0 i c = 0
Si c = 0
Si b= 02.- Estudi de la solució l'equació completa.
3.- Estudi del número de solucions segons el valor del discriminant.
4.- Estudi de les propietats de les solucions
5.- Representació gràfica de l'equació.
6.- Estudi dels paràmetres característics en la representació gràfica:
o Valor de la a
o Valor de la b
o Valor de la c
o Punts singulars: vèrtex, punt de tall eix x, punt de tall eix y
Una equació és de segon grau amb una incògnita si, un cop efectuades les operacions i reduïts els seus termes semblants, el terme de major grau que conté és de grau 2.
Cada valor de la incògnita que verifica l'equació de segon grau és una solució o arrel d'aquesta equació.
Observa que en substituir la x per 4 en x2-2x+1=9 obtenim 42-2·4+1=9, és a dir, x=4 verifica l'equació. Direm que 4 és una solució o una arrel d'aquesta equació.
Prova ara de substituir alguns valor per tal de trobar la solució:
1.- Estudi de les solucions de l'equació reduïda
Una equació de segon grau amb una incògnita es pot expressar mitjançant una equació del tipus a·x2+b·x+c=0, en què, a, b i c són nombres reals i a és diferent de zero.
Si els coeficients b i c són diferents de 0 direm que l'equació de segon grau és completa i, si algun dels coeficents b o c prenen el valor 0, direm que és completa.
Així estudiem ara alguns exemples:
Proveu ara de solucionar els diferents tipus d'equacions reduides, i desprès cliqueu a sobre la fletxa per tal de comprovar-ho si ho heu fet bé:
- equació reduida amb b=0 i c=0:
- equació reduida amb c=0:
- equació reduida amb b=0:
2.- Estudi de la solució l'equació complerta.
Les solucions d'una equació de segon grau amb una incògnita, a·x2+b·x+c = 0, vénen donades per la fòrmula:
Com que ara ja saps com trobar les solucions de qualsevol equació de segon grau, prova amb aquestes, i desprès clica sobre la fletxa per tal de veure si ho has fet bé:
3.- Estudi del número de solucions segons el valor del discriminant.
L'expressió b2 - 4·a·c que apareix en la fórmula general per a resoldre equacions de segon grau rep el nom de discriminant de l'equació i el seu valor numèric permet determinar el nombre de solucions de l'equació sense que calgui resoldre-la. Fixa't en la taula següent:
El que ara hauràs de fer es primer calcular el discriminant de les següent equacions de segon grau i desprès trobar les solucions per comprovar que el número de solucions que has trobat es correcte segons el signe del discriminant, segueix el següent exemple de la Wiris:
Igual que fins ara, primer prova de solucionar-ho tu i desprès clicar a la fletxa per comprovar la solució:
4.- Estudi de les propietats de les solucions
Existeixen unes relacions entre les solucions d'una equació de segon grau i els seus coeficients. A continuació les veurem i observarem alguna de les seves utilitats,
- Suma i producte de les solucions
Si x1 i x2 són les solucions de l'equació de segon a·x2 b·x+c = 0, es compleix que:
Fixa't amb aquest exemple per a desprès provar-ho tot sol:
Ara, et toca a tu:
a)
b)
c)
- Determinació de l'equació de segon a partir de la suma i del producte de les seves solucions:
Si S és la suma de les solucions d'una equació de segon grau i P és el seu producte, podem escriure aquesta equació de la forma:
Fixa't com podem trobar l'equació a partir de la suma i el producte de solucions:
Ara intenta fer-ho tu:
a) S= -11 i P=-12
b) S=2 i P= 3/4
5.- Representació gràfica de l'equació.
Per representar gràficament una equació de segon grau hem de contruir una taula de solucions assignant valor arbitraris a la x i calculant els corresponents a la y.
Tot seguit representem els punts en uns eixos de coordenades i unim els punts mitjançant una corba, clica a la fletxa per tal de veure la gràfica
La proposta més interesant és, que ara ho provis de fer amb aquests dos exemples:
6.- Estudi dels paràmetres característics en la representació gràfica:- Valor de la a
Si a>0 les branques van dirigides cap amunt i s'anomena paràbola còncava. Si a<0 les branques van dirigides cap avall i s'anomena paràbola convexa. A mesura que el valor absolut de a augmenta, la paràbola es tanca, i a mesura que aquest valor disminueix, la paràbola s'obre.
Observa el següent exemple:
- Valor de la bLa paràbola y = a·x2 + b·x té la mateixa forma que y = a·x2 però desplaçada -d unitats horitzontalment , per tant la ordenada del vèrtex serà la mateixa per a les dues paràboles. Aquest paràmetre el causant del desplaçament horitzontal de la paràbola. Observa la següent animació i desprès practica clicant a sobre la fletxa:
- Valor de la c
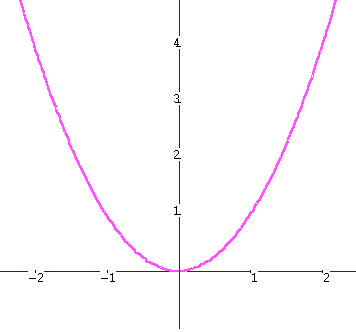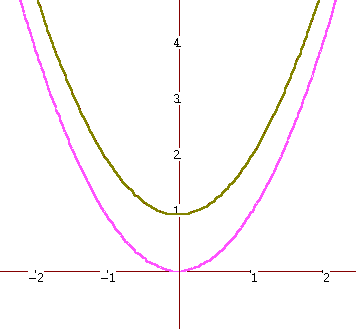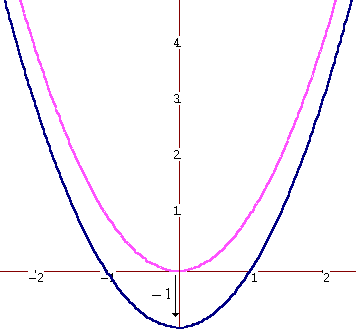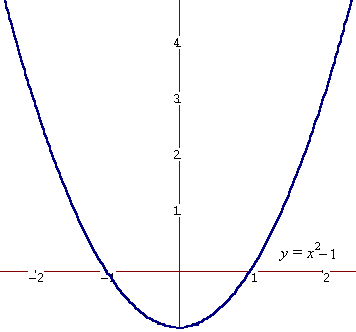
La paràbola y = a·x2 + b·x + c té la mateixa forma que y = a·x2 + b·x però desplaçada c unitats verticalment, per tant l'abscissa del vèrtex serà la mateixa per a les dues paràboles.
Primer observa aquesta animació i tot seguit, clica a la fletxa per pràcticar-ho:
- Vèrtex de la paràbola
L'abscissa x i l'ordenada y del vèrtex de y = a·2 + b·x+c resulta:
Calculem ara el vèrtex de la següent paràbola i observa-ho a la representació gràfica:
Per acabar, un parell d'exercici de determinar el vèrtex de les següents equacions: