|
- Euclides,
Arquímedes y Apolonio de Perga, fueron las tres
grandes figuras matemáticas del helenismo.
- Euclides representa la sistematización del saber
matemático,
- Arquímedes, fue el genio polifacético por
excelencia, y
- Apolonio, el menos conocido, fue desde el punto de vista
matemático el verdadero especialista en geometría.
Su obra, Las Cónicas, no se conoció en el
mundo occidental hasta el año 1710, cuando fue publicada
por Edmond Halley. Sobre
su vida se sabe muy poco: Nació, a mediados del siglo III
a. C., en Perga, y parece que pasó largo tiempo
en Alejandría, cuya Biblioteca constituía
en aquel tiempo
el centro del saber occidental.
|
|
- Apolonio
supera extraordinariamente todo el conocimiento sobre cónicas
(elipse, hipérbola, parábola)
que hasta entonces se tenía y lo presenta de un modo mucho
mejor organizado. Sus conocimientos y hallazgos sobre cónicas
los reune en una obra, Las Cónicas, que presenta
en ocho volúmenes, de los que los cuatro primeros no son
más una introducción elemental y parecen recoger
todo lo que, probablemente, se sabía hasta entonces sobre
las cónicas; en ellos se exponen: modos de obtener las
cónicas y propiedades básicas, diámetros,
ejes y asíntotas, teoremas notables, propiedades de los
focos e intersección de dos cónicas.
- En el libro
I define las cónicas como resultado de seccionar con un
plano un cono circular de dos hojas (figura a la derecha). En
este mismo libro considera también centro, ejes, diámetros
conjugados, tangentes, etc. y aborda incluso el problema de construir
una cónica a partir de diversos elementos suyos.
|
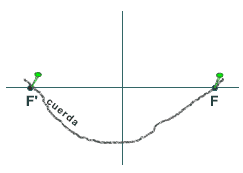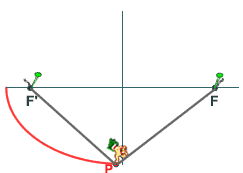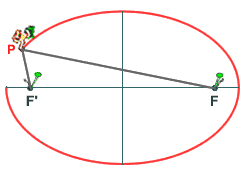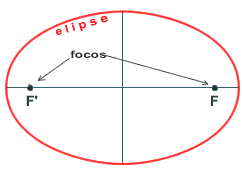
Figura 2
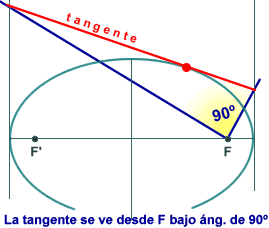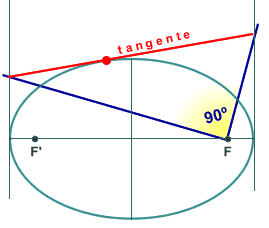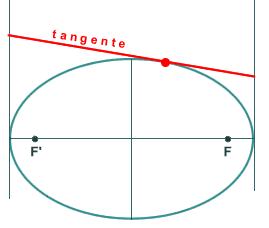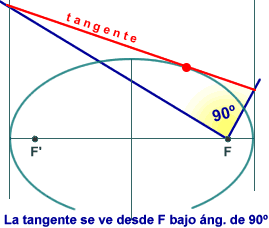 Figura 3
Figura 3
|
- En el libro
II estudia fundamentalmente las propiedades de las asíntotas
de la hipérbola. Al final, trata también el siguiente
problema:Trazar una tangente que forme un ángulo dado
con el diámetro que pasa por el punto de contacto.
- En el libro
III, uno de los de más valor, aparece ya lo que hoy solemos
dar como definición de elipse, o sea la elipse
es el
þ
lugar geométrico de los puntos cuya suma de distancias
a dos puntos fijos, F y F', es constante (figura 2).
En este mismo libro se estudian también las relaciones
de triángulos y cuadriláteros determinados por tangentes
y diámetros conjugados, aparece también la hipérbola
como lugar de los puntos cuyo producto de distancias a dos
rectas fijas es constante, y aparecen interesantes propiedades
sobre los focos, como por ejemplo la de la figura 3:
þ
desde un foco F de la elipse, se ve bajo ángulo recto
el segmento de cualquier tangente comprendido entre las tangentes
en los vértices.
- En cuanto
al libro IV, en él estudia el número de puntos de
intersección de las cónicas. Contiene 55 proposiciones
y es de destacar el hecho de que las 23 primeras aparezcan hechas
por reducción al absurdo.
|
|
Los resultados
que se exponen en los libros V, VI y VII son descubrimientos del
mismo Apolonio y se refieren a:
- Segmentos
de máxima y mínima distancia a las cónicas,
normal, centro de curvatura (libro V, considerado como el
mejor y más original, en el que introduce ya, a su modo,
nociones tales como normal a una curva, evoluta, centro de curvatura,
etc,.. y obtiene ya esos elementos para las cónicas de
la manera más rigurosa).
- Igualdad
y semejanza de las secciones cónicas (libro VI, en
el que resuelve muy elegantemente el siguiente problema: dados
una cónica y un cono circular recto, hallar una sección
del cono que sea igual a la cónica.).
- Relaciones
métricas sobre diámetros conjugados, áreas,
etc. (libro
VII).
Y sobre el libro
VIII, se desconoce aún su contenido.
|

|
|
|