|
- Arquímedes
fue sin duda la figura máxima de la matemática griega y uno de
los más grandes científico-matemáticos de todos los tiempos. Nació
en Siracusa (Sicilia) el año 287 a. C., se educó en Alejandría
(Egipto), pero pronto volvió a su ciudad natal, donde realizó
hasta su muerte un intenso trabajo científico. Al final de su
vida participó en la defensa de Siracusa contra los romanos, construyendo
armas de guerra (catapultas, sistemas de espejos para incendiar
naves,...) con las que se logró retrasar notablemente la conquista
de la ciudad. No obstante, en el año 212 a.C., la ciudad cayó
en poder de las tropas del general Marcelo, y durante el
consiguiente saqueo, Arquímedes murió atravesado por la
espada de un soldado romano, aun a pesar de que Marcelo,
según cuenta Plutarco, había ordenado que se respetara
su vida.
|
|
-
Los trabajos de Arquímedes son auténticas memorias científicas,
trabajos originales en los que siempre se aportan elementos nuevos,
no conocidos hasta entonces. En ellos siguió rigurosamente el
método euclídeo de fijar exactamente las hipótesis y enunciar
y demostrar cuidadosamente los teoremas subsiguientes. Toda su
obra fue escrita en varios tratados; De la esfera y el cilindro,
De los conoides y de los esferoides, Cuadratura de la parábola,
De la medida del círculo y El Arenario son son sus principales
escritos sobre matemáticas, pero Arquímedes tiene también
destacados escritos sobre estática, como el titulado Del
equilibrio de los planos, en el que enuncia la ley de equilibrio
de la palanca, y en hidrostática, como el titulado De
los cuerpos flotantes, en el cual estudia científicamente
el equilibrio de los cuerpos sumergidos y enuncia el que conocemos
hoy com principio de
Arquímedes. Se dice que este descubrimiento lo hizo mientras
se bañaba, pensando en cómo resolver un problema que le había
encargado el rey Herón de Siracusa.
|
-
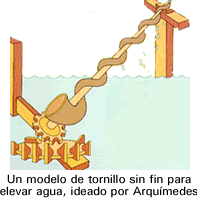
En mecánica, Arquímedes hizo numerosos trabajos; definió,
por ejemplo, la ley de la palanca y se le tiene por el inventor
de la polea compuesta. Durante su estancia en Egipto inventó también
el tornillo sin fin para elevar el agua de nivel.
Arquímedes pasó la mayor parte de su vida en Siracusa, dedicado
a la investigación y los experimentos. Aunque no tuvo ningún cargo
público, durante la conquista de Sicilia por los romanos se puso,
como hemos dicho, a disposición de las autoridades de la ciudad
y muchos de sus instrumentos mecánicos se utilizaron en la defensa
de la ciudad. Entre la maquinaria de guerra cuya invención se
le atribuye está la catapulta y un sistema de espejos
que incendiaba los barcos enemigos al enfocarlos con los rayos
del sol.
|
|
- En
el campo de las matemáticas puras, se anticipó a muchos de los
descubrimientos de la ciencia moderna, como el cálculo integral,
con sus estudios de áreas y volúmenes de figuras sólidas curvadas
y de áreas de figuras planas. Demostró, por ejemplo, que el
volumen de una esfera es dos tercios del volumen del cilindro
que la circunscribe, encontró y demostró las fórmulas del
área del círculo, la de la superficie de la esfera,
la del área encerrada por un segmento de parábola, etc.
Y no sólo eso, sino que, además, ideó métodos mecánicos para obtener
resultados matemáticos que luego demostraba rigurosamente siguiendo
métodos de demostración de matemáticos anteriores tales como Euclides
o Eudoxo (método de exhaución).
- A
la derecha puede verse el método que siguió para obtener aproximaciones
del número pi (pase el ratón por encima):Construyó
polígonos regulares inscritos y circuncritos a una circunferencia,
estimando así la longitud de ésta mediante los perímetros de aquéllos.
Así, llegando a trabajar hasta con el polígono de 96 lados, obtuvo
que pi estaba entre las fracciones 223/71 y 22/7, es decir,
entre 3'1408... y 3'1428..
|
|
- Pero, de
todos sus logros, quizá su obra maestra sea la titulada Sobre
la esfera y el cilindro, en la cual determina áreas y volúmenes
de esferas y cuerpos relacionados, consiguiendo así para sólidos
tridimensionales lo que ya había logrado para figuras planas en
su escrito titulado Medida del círculo. Fue al menos la
obra que el propio Arquímedes consideraba como su gran
triunfo, dado que pidió que se grabara en su tumba la imagen de
una esfera y un cilindro circunscrito, con la inscripción Vcil
= 1'5 Vesf.
- También se
interesó Arquímedes por cuestiones aritméticas, como demuestra
su obra El Arenario, en la que pretende probar que el número
de granos de arena que llenara todo el universo podría contarse,
e incluso nombrarse. El interés de esta obra es doble: Por una
parte crea un sistema de numeración propio para manejar grandes
números, y por otra, es el único escrito en el que demuestra poseer
buenos conocimientos astronómicos, dando incluso un método para
calcular el diámetro aparente del Sol.
|
|
|
 Ý
Ý
|
|
Sobre
todo cuerpo sumergido en un líquido actúa una fuerza hacia
arriba (empuje) cuyo valor es igual
al peso del líquido que ha desalojado (figura
a la derecha).
|
|
| |
Leyenda
asociada al principio de Arquímedes.
Se cuenta
que el rey Herón de Siracusa le había entregado a un platero
una cierta cantidad de oro para con ella le hiciera una corona.
Cuando estuvo terminada, se decía que el platero había sustituido
una parte del oro por una cantidad equivalente de plata, devaluando
con ello la corona y engañando, pues, al rey. El rey encargó
a Arquímedes que descubriera si había sido engañado. Éste,
absorto en el problema, descubrió un día la solución mientras
se bañaba y, saltando del baño, corrió desnudo por las calles
de Siracusa gritando: ¡eureka! ¡eureka!. Había descubierto
que, pesando el volumen de agua desplazado por la corona al
sumergirla, podía saber si contenía la misma cantidad de oro
que el rey le había dado. |
|
|
|
Imaginemos
una línea quebrada ABC (segmento AC doblado en un punto
B). Su punto medio, M, puede hallarse por el siguiente procedimiento:
- Se
traza el arco de circunferencia que pasa por los tres
puntos A, B y C.
- Se
halla el punto medio, M', del arco de circunferencia AC.
- Entonces,
la perpendicular a BC trazada por M' da sobre BC el punto
medio, M, de la cuerda doblada ABC.
|
|
| Curiosamente,
utilizando este teorema, puede deducirse la fórmula trigonométrica
sen(x-y) = senx·cosy - cosx·seny |
|

|
|
Cuando se dice que un barco
desplaza 20 toneladas, ¿podemos saber el peso total
del barco?. ¿Qué empuje experimenta el barco
hacia arriba mientras navega?
|
|
|
|