Por definición, distancia de A a B es el módulo del vector .

    Suponiendo A = (a₁, a₂, a₃) y B = (b₁, b₂, b₃),

d(A,B) = =

¨ De un punto, A, a un plano p.

(figura)

    Generalmente, podrás hallar d(A, p) de dos formas:

1. Calculando primero A’, y luego d(A,A’). (A’ se hallará como intersección de p con la recta por A perpendicular a p)
2. Aplicando la siguiente fórmula:

¨  De un punto, A, a una recta r.

    La menor de las distancias de A a los puntos de r se llama distancia del punto A a la recta r.

    Si A’ indica la proyección de A sobre r, entonces d(A,A’) es, precisamente, la distancia de A a r.

    Generalmente, podrás hallar d(A,r) de dos formas:

    1. Calculando primero A’, y luego d(A,A’). (A’ se hallará como intersección de r con el plano por A perpendicular a r)

    2. Aplicando la fórmula:  (X indica un punto cualquiera de r)

¨ De una recta, r, a un plano, p, paralelo a ella.

    Para hallar d(r, p), deberás, pues, tomar en r un punto A y, luego, calcular d(A, p).

¨ Las distancias entre rectas paralelas, y entre planos paralelos, son similares a este último caso.

¨ Damos aparte el caso de distancia entre rectas que se cruzan.

¨ Entre dos rectas, r y s, que se cruzan.

1. Hallando los puntos de corte A_r y A_s (ve método 2, más adelante)
   
   
2. Aplicando la fórmula
                         
   (X_r y X_s indican puntos, elegidos libremente, en r y s, respectivamente)
   
   
   
   

Dos formas de hallar la perpendicular común

1. Si r y s vienen dadas en forma general, suele convenir usar la ecuación del haz de planos como sigue.

Caso práctico:

1º Hallamos el vector , que será director de la perpendicular común.
    En este caso, da . (Como sólo lo usamos como director, podemos tomar )

2º La perpendicular común es el corte de dos planos: uno, p_r, conteniendo a r y otro, p_s , conteniendo a s (fig. 2)

Plano p_r:

3º El vector debe ser ortogonal a los vectores y

, ,

, ,

Por tanto, . Finalmente,

Ecuaciones perpendicular común

2. Si r y s vienen dadas en forma paramétrica, suele convenir el cálculo de los puntos de corte, A_r y A_s.

Caso práctico:

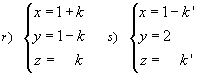
1º Los puntos A_r y A_s se podrán poner así: A_r = (1+k, 1-k , 1), A_s = (1-k’, 2, k’ ). Con lo cual, el vector director de la perpen-dicular común es: .

2º Como debe ser ortogonal a ,

De ese sistema, salen k y k’, y por tanto, los puntos A_r y A_s.

Perpendicular común: recta t

Figura 2