Estudiarem només les posicions relatives a
partir de les equacions generals (o implícites)
Posicions
de dos plans: 
Per al sistema format per les dues equacions, 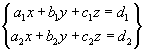 ,
hi ha les següents possibilitats:
,
hi ha les següents possibilitats:
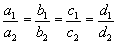 .
Llavors els plans coincideixen (fig. 1)
.
Llavors els plans coincideixen (fig. 1)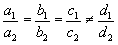 .
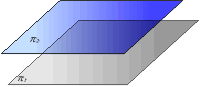
Llavors son plans paral·lels, i diferents (fig. 2)
.
Llavors son plans paral·lels, i diferents (fig. 2)
- En qualsevol altre cas, el rang del sistema és
2, i llavors els plans defineixen una recta (fig. 3)

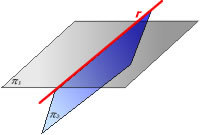
Posicions
de dos rectes:
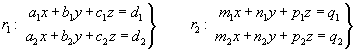
Anomenarem A la matriu del sistema format por
aquestes quatre equacions, i A’ l'ampliada.
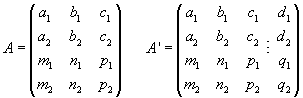
Aquestes són les possibilitats:
- rang(A) = 2, rang(A’)=2. Llavors, són dos
rectes coincidents.
- rang(A) = 2, rang(A’)=3. Llavors, són dos
rectes paral·leles, diferents.
- rang(A) = 3, rang(A’)=3. Llavors, són dos
rectes secants; el punt de tall és la solució del sistema.
- rang(A’)=4, és a dir, Det(A’) ¹
0. Llavors, es diu que les rectes
es creuen.
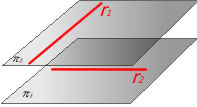
Dos rectes que es creuen sempre podran situar-se
en dos plans paral·lels. A més, aquest és l'únic cas en
què no existeix un pla que contingui les dues rectes (rectes
no coplanàries)
Posicions
d'una recta i un pla: 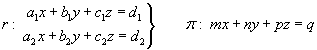
Anomenarem A la matriu del sistema format por
aquestes tres equacions, i A’ l'ampliada.
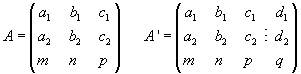
Aquestas són les possibilitats:
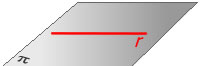
- rang(A) = 2, rang(A’)=2. Llavors, la recta està
continguda al pla (fig. 1).
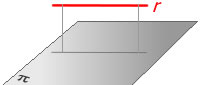
- rang(A) = 2, rang(A’)=3. Llavors, la recta és
paral·lela al pla, i no inclosa en ell (fig. 2).
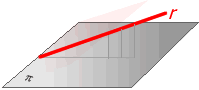
- rang(A) = 3, rang(A’)=3. Llavors, es diu que la
recta és secant al pla.
El punt de tall és la solució del sistema (fig. 3)
És important adonar-se que el paral·lelisme
de recta i pla es presenta exactament quan Det(A) = 0.
Posicions
de 3 plans:
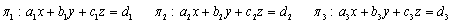
Anomenarem A la matriu del sistema format por
aquestes tres equacions, i A’ l'ampliada.
Aquestes són les possibilitats:
- rang(A) = 1, rang(A’)=1. Llavors, els 3 plans
coincideixen.
- rang(A) = 1, rang(A’)=2. Llavors, són 3
plans paral·lels (Dos d'ells poden coincidir.)
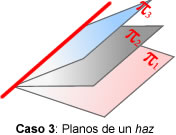
- rang(A) = 2, rang(A’)=2. Llavors, els 3 plans
contenen una mateixa recta (plans d'un feix)
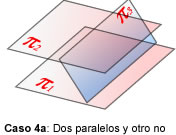
- rang(A) = 2, rang(A’)=3. Llavors, hi ha dues possibilitats:
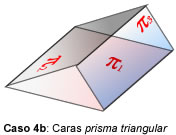
a) Hi ha 2 plans paral·lels, i altre
els talla b) Els tres són cares
d'un prisma triangular
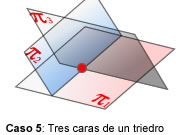
- rang(A) = 3, rang(A’)=3. Llavors, els plans tenen
exact.un punt comú (caras de trièdre)


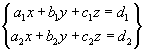 ,
hi ha les següents possibilitats:
,
hi ha les següents possibilitats:


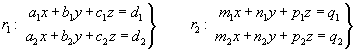
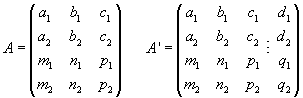

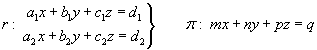
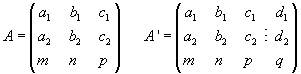
![]()


![]()



