|
- Hacia
el año 332 a.C., Alejandro Magno fundó
la ciudad de Alejandría, que tras la creación de su gran Biblioteca,
llegó a ser centro mundial de la cultura. Uno de tantos eruditos
atraídos a ella fue un tal Euclides. Se sabe poco sobre
él, aunque parece cierto que se formó en la Academia con discípulos
de Platón y que enseñó matemáticas en Alejandría, donde
fundó una escuela. Pero, en todo caso, su influencia ha sido decisiva
a través de su obra cumbre, Los Elementos, que ha sido
siglo tras siglo como la biblia de las matemáticas, usándose incluso
como libro de enseñanza; por su difusión (unas 2000 ediciones)
podría rivalizar con obras cumbre de la literatura universal,
como la Biblia, la Divina Comedia, el Quijote,
etc.; el hecho de que contenga un estilo a veces poco coherente
ha llevado a creer a algunos que Euclides era en realidad
un grupo de matemáticos.
|
|
-
Los Elementos es un tratado de 13 libros que suelen asociarse
generalmente a la geometría, pero en realidad engloba 465 proposiciones,
o teoremas, sobre geometría plana, sólidos y teoría de números.
- En
los libros I, II, III y IV, Euclides agrupó las proposiciones
fundamentales relativas a las figuras planas más simples: segmentos,
ángulos, rectas paralelas, triángulos, paralelogramos, cuadrados
y círculos. Tras dar 23 definiciones (punto, línea,
línea recta, etc) Euclides da una lista de 5 postulados,
o axiomas, que considera evidentes por sí mismos e independientes,
es decir, ninguno de los cinco puede deducirse lógicamente de
los otros cuatro. Desde muy pronto los matemáticos no vieron tan
clara la aceptación sin demostración del quinto de dichos postulados
(al que llamaron postulado
de las paralelas) y durante siglos fueron muchos los que
intentaron demostrarlo; diríase que ni el propio Euclides
estaba a gusto con su quinto postulado,
ya que en su demostraciones intenta evitar su utilización, como
lo demuestra el hecho de que no lo use hasta la proposición número
28.
- Los
libros V y VI se dedican a la semejanza y estudian las
razones y las proporciones, y los libros VII, VIII y IX se conocen
como "libros aritméticos", porque en ellos se estudia
teoría de números enteros.
- El
libro X, quizá el más perfecto de todos, se dedica al estudio
de los números irracionales más simples.
- Y
los libros XI, XII y XIII se dedican a geometría espacial; el
último de ellos se refiere, concretamente, a la inscripción dentro
de una esfera de los cinco poliedros regulares: tetraedro,
cubo, octaedro, dodecaedro e icosaedro.
- Los
Elementos, ni por su contenido, ni por su orientación,
son fruto exclusivo de Euclides: Su contenido procede
en gran parte de los pitagóricos y de Eudoxo (astrónomo
y matemático griego que realizó importantes aportaciones en geometría
y expuso la primera explicación sistemática de los movimientos
del Sol, la Luna y los planetas); y en cuanto a su orientación,
están influidos por Platón (del que Euclides tomó
el aprecio de la ciencia independientemente de su finalidad práctica)
y por Aristóteles, de quien tomó el riguroso método deductivo,
la separación entre principios y teoremas y la distinción
de los principios entre definiciones y axiomas (enunciado
que se acepta sin demostración)
- La
genialidad de Euclides no estuvo, pues, en crear matemáticas
nuevas (se acepta que sólo unos pocos teoremas de los Elementos
son originales de Euclides) sino la de presentar de una
manera clara, organizada y lógica, la geometría y la aritmética
hasta entonces conocidas. Esa forma de presentación -conceptos,
axiomas, enunciados, demostraciones- se ha mantenido hasta
nuestros días. Como prueba de la elegancia de sus demostraciones,
damos la del teorema
de infinitud del conjunto de los números primos (números mayores
que 1 que sólo son divisibles por 1 y por ellos mismos)
|
 Ý
Ý |
|
Si
una recta corta a otras dos y forma dos ángulos internos que
suman menos que dos ángulos rectos, en caso de prolongar éstas
indefinidamente se cortarán del lado en que la suma de los
ángulos internos es menor que dos rectos.
|
|
| Es
decir, las líneas rectas de la figura a la derecha se cortan
del lado derecho de la recta r. |
|
Otros enunciados equivalentes
al anterior.
- Dadas dos
rectas paralelas, si una recta corta a una de ellas, corta
también a la otra (axioma de Proclo).
- Dos rectas
paralelas son siempre equidistantes.
- Por un punto
exterior a una recta dada sólo pasa una paralela a dicha
recta (axioma de Playfair).
- La suma
de los tres ángulos de un triángulo es 180º.
|
|
|
El quinto postulado trajo
cola.
A lo largo de la historia de las matemáticas,
quizá sea el quinto postulado el enunciado más controvertido.
El problema no surge porque alguien dude de la verdad de
su contenido; realmente, siempre se aceptó que era una necesidad
lógica. Lo que siempre se discutió fue su caracter de postulado;
ya el escritor clásico Proclo advertía de que era
más bien un teorema y, por tanto, debería ser demostrado
a partir de los otros cuatro.
Hasta el siglo XIX, innumerables matemáticos
intentaron demostrarlo, pero nunca lo consiguieron, y aunque
dieron con numerosos enunciados equivalentes a él, la búsqueda
de una demostración continuó, muchas veces inluso por el afán
de alcanzar fama eterna. Ya entrado el siglo XIX, tres matemáticos,
Gauss, Bolyai y Lobachevski, independientemente,
llegaron a la conclusión de que podía obtenerse una nueva
geometría, de toda consistencia lógica, sin aceptar el postulado
de las paralelas; más exactamente, una geometría, igual
en todo a la de Euclides, pero en la que los ángulos
de un triángulo sumaran menos de 180º. Fue éste el primer
invento de geometría no euclídea; algunos años
después, otro matemático, Riemann, creó otra geometría
no euclídea suponiendo rectas no infinitas y en la cual resultaba
que la suma de los ángulos de un triángulo superaba 180º.
|
 Ý Ý |
|
Existe
una infinidad de números primos.
|
| Para
demostrar el teorema, Euclides utilizó algunas proposiciones
que ya había demostrado anteriormente, tales como |
|
|
- Si un número es divisor
de otros dos, también lo es de la diferencia de ambos.
|
|
A partir de ahí, se preguntó qué ocurriría
si hubiese sólo unos cuantos números primos; por ejemplo,
si hubiese sólo 3 números primos a, b, c. Él
pensó: Si eso ocurriese, entonces con el número N=a·b·c+1
podría pasar sólo una de estas dos cosas:
-
Que
N fuese a su vez un número primo. Esto es imposible,
ya que entonces no habría sólo tres primos, sino al menos
cuatro.
- Que
N no fuese primo, sino compuesto.
Entonces N tendría algún divisor primo, d. No es
posible, pensó, que el d sea igual al a, ya
que entonces, de la igualdad N-a·b·c = 1 resultaría
que el a es divisor del 1, cosa imposible pues el
1 no tiene divisores. Análogamente, d no puede ser
ni b, ni c, luego d es un primo distinto
de a, b y c. Ya no habría sólo 3 primos, sino
como mínimo cuatro.
En definitiva,
¿qué ocurre? ¿Estamos en un callejón sin salida? En absoluto;
lo único que ocurre es que es imposible que haya sólo 3
números primos, pues si suponemos que hay sólo tres, siempre
podemos encontrar uno más. A idéntica conclusión se habría
llegado de haber supuesto que sólo hay cuatro, o cinco, o
cualquier número finito de primos: Por muchos que cojamos,
siempre llegaremos a la conclusión de que hay alguno más,
es decir, sólo vale la afirmación de que hay infinitos
primos.
|
 |
|
La demostración anterior es
completamente ilustrativa del llamado método de razonamiento
indirecto, o de reducción al absurdo: consiste
en suponer cierto el contrario de un enunciado y llegar a
un imposible razonando por las vías de la lógica; entonces,
sólo cabrá la posibilidad de que dicho contrario no sea cierto
y, por tanto, el enunciado sea verdadero.
Te proponemos que resuelvas
por ese método el siguiente acertijo:
|
- Tres muchachas, Nuria,
Sara y Raquel, tienen los ojos vendados y un
diminuto sombrero en la cabeza, el cual puede ser rojo
o negro. Ninguna ve su propio sombrero. Se les dice
que, al quitarles las vendas, levanten una mano si ven al
menos un sombrero rojo, y las dos, quien llegue a la conclusión
de que su sombrero es rojo. Supongamos ahora que en realidad
les hemos puesto los tres sombreros rojos. ¿Cómo puede una,
por ejemplo, Nuria, razonar que su sombrero es rojo?.
|
|

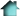
|
|
|