Llamaremos
- D3 al conjunto de los puntos del espacio ordinario,
- V3 al conjunto de los vectores libres del espacio ordinario
- La estructura de espacio vectorial de V3,
aplicada en el conjunto D3,
permite (¡recuérdalo!)
estudiar los problemas de indicencia,
intersección y paralelismo (llamados
de tipo afín).
- Añadiendo a V3
el concepto de producto escalar, se pueden estudiar fácilmente
problemas de perpendicularidad, distancias, ángulos, áreas
y volúmenes (llamados problemas
de tipo euclídeo).
Memoriza, pues, el siguiente esquema:
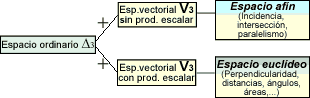
Letras como A, B, etc., indicarán puntos;
r, s,... indicarán rectas, y las letras p,
p’, etc., planos. En todo
momento, supondremos elegida una referencia ortonormal.
Vector ortogonal a
un plano
- Si v1, v2
es un par de vectores directores de un plano, p,
el vector np
= v1 Ù
v2 , o cualquier múltiplo
suyo, suele llamarse vector ortogonal al plano.
- Si p
es mx + ny + pz = q, un vector ortogonal es np
= (m, n, p)
|

|
Perpendicularidad
de ...
|
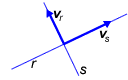
Dos rectas se llaman perpendiculares si tienen vectores directores ortogonales.
r ^ s ÜÞ vr·vs = 0 |
|
|
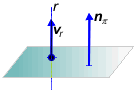
Una recta, r, es perpendicular a un plano, p, si el vector director de r y el vector ortogonal a p son l.d. (o sea, proporcionales)
r ^ p ÜÞ vr = k np |
|
|
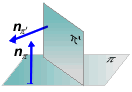
Dos planos son perpendiculares si sus vectores ortogonales son
ortogonales entre sí
p
^
p’
ÜÞ
np·
np’
= 0
Si los planos son 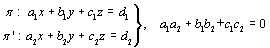
|
|
Ejercicios
propuestos: 2
(pág. 141), 6, 7 (pág. 143), 10, 11, 12 (pág.
143) (libro EDEBÉ, libro Matemàtiques II)


