|
- Sobre
el año 600 a.C. vivió el gran Tales de Mileto, a quien
se considera generalmente como el primer matemático demostrativo
del que se tiene noticia. La siguiente figura importante de las
matemáticas griegas fue Pitágoras, nacido en Samos en el
año 572 a.C.
- Pitágoras
vivió en en la parte sur de la actual Italia, en la
ciudad griega de Crotona, y allí fundó una sociedad secreta
de estudios que conocemos con el nombre de escuela pitagórica.
Los pitagóricos vivían en comunas y se regían por unas
normas extraordinariamente estrictas, hasta tal punto que, según
se cuenta, tenían prohibida la ingestión de ciertos alimentos
(por ejemplo, carne, judías, ...), y la divulgación de sus descubrimientos
la pagaban con la vida; realmente, fueron ellos los difusores
de la doctrina de Pitágoras, ya que de éste
no se conserva ningún escrito (quizá por eso, hay
quien ha llegado a dudar incluso de su existencia)
- Destacaron
en música, astronomía y, sobre todo, en matemáticas. En su contemplación
del mundo, consideraban el número entero como la esencia de todas
las cosas: "todo es número", era su lema. Por
encima de cualquier otra, son de destacar dos grandes aportaciones:
el famoso enunciado conocido por "teorema
de Pitágoras" y el descubrimiento de las cantidades
irracionales, es decir, cantidades que no podían ser medidas mediante
ningún número entero o fraccionario; concretamente, descubrieron
que la diagonal de un cuadrado y el lado no podían ser medidos
a la vez, y exactamente, usando una unidad de medida común; expresaron
este hecho diciendo que ambas longitudes son inconmensurables
(no medibles con una unidad común). Esto supuso para ellos un
verdadero mazazo, no sólo porque usaban la idea de la conmensurabilidad
de segmentos en sus demostraciones geométricas, sino porque, además,
derribaba toda su teoría filosófica sobre el papel central del
"número entero"; cuenta la leyenda que, exasperados
por semejante perturbación, arrojaron mar adentro a Hippaso,
su descubridor
- En
cuanto al famoso teorema, se sabe que, más de 1000 años antes,
los babilonios ya lo conocían; sin embargo, su demostración es
atribuída de forma unánime a los pitagóricos. Cuenta la leyenda
que Pitágoras ordenó sacrificar un buey a los dioses para celebrar
el descubrimiento de la demostración. Aquí os damos 3 demostraciones
gráficas distintas de dicho teorema; la última es debida a Gardfield,
el vigésimo presidente de los Estados Unidos de América. La primera
de las tres ya la habréis visto en la presentación.
|
| |
 Ý
Ý
|
|
| |
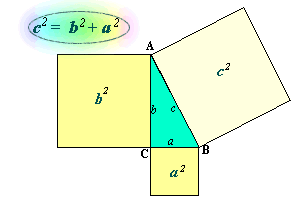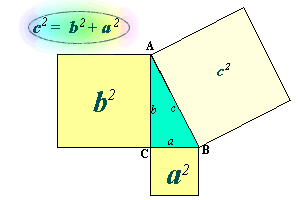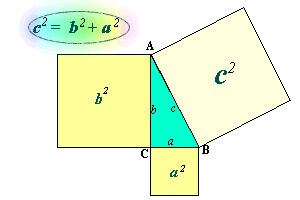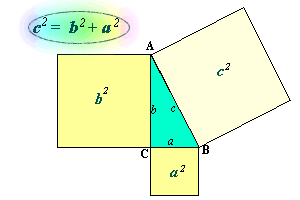
En
todo triángulo rectángulo, ABC, el cuadrado del lado mayor (hipotenusa)
da lo mismo que la suma de los cuadrados de los lados menores (catetos).
Es decir, el cuadrado construido sobre la hipotenusa da la misma
superficie que la suma de los cuadrados construidos sobre los catetos.
NOTA.
Los escolásticos consideraban el teorema de
Pitágoras como la frontera entre la geometría accesible
a cualquiera y la geometría avanzada, o sea, innaccesible
a la majoría; por eso, le llamaban el "puente de
los asnos"
|
|
|
| |
|
|
| |
Demostración
2
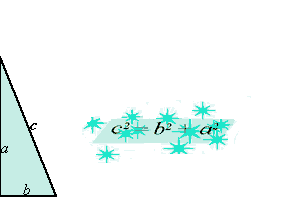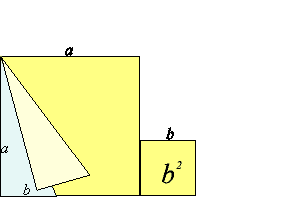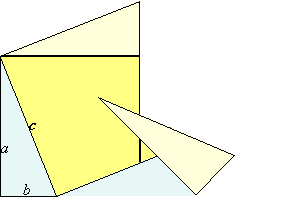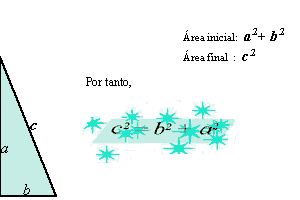
|
Demostración
3
(Garfield,
20º presidente de los E.E.U.U.)
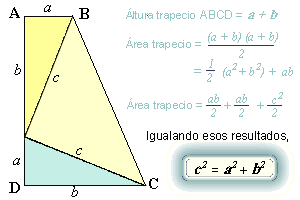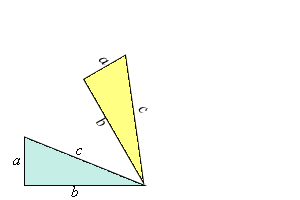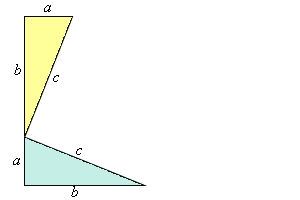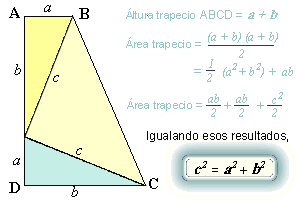
|
|

|
|
|