Llegeix i memoritza
És molt important que memoritzis
| • | El concepte de repartiment directament proporcional i les proporcions que hi intervenen per fer-ho. |
| • | La forma general de sumar fraccions. |
| • | Què vol dir fer un repartiment de tipus inversament proporcional i quines proporcions intervenen per fer-ho. |
Repartiments directament proporcionals
En moltes situacions de la vida es presenta la necessitat de fer repartiments directamente proporcionals. Així passa, per exemple, sempre que s'han de repartir beneficis d'un negoci entre varis socis que han aportat a la constitució de l'empresa quantitats diferents.
Un exemple molt clar: Si he comprat un dècim de loteria amb un amic, però jo he posat 15 € i ell només 5 €, aleshores, en cas que toqui, jo me n'hauria d'emportar el triple que ell; si en toquessin 1000 €, jo me n'hauria d'emportar 750 € i ell, 250 €. Així, estaríem fent un repartiment de 1000 € en parts directament proporcionals a 15 i 5.
Però, parlant ja en abstracte, què vol dir realment fer repartiments directament proporcionals?.
| Repartir una quantitat Q en parts directament proporcionals a dos nombres a i b vol dir |  |
||
| • |
dividir Q en dos
parts, x i y, de manera que |
||
Com podeu veure en el requadre a la dreta, per repartir, per exemple, 20 en parts proporcionals a 2 i 3, s'han de resoldre dues proporcions, que són les següents: |
|||
| |
|||
| Anàlegament, per dividir la quantitat Q en parts proporcionals a dos nombres, a i b, s'hauran de resoldre les proporcions següents: | |||
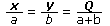 |
|||
En general, els repartiments es podran fer relatius a més de dos nombres. Es poden fer repartiments proporcionals a tres nombres, a, b i c; a quatre nombres a, b, c i d, etc. En tot cas, el mètode és sempre el mateix i es basa en resoldre diverses regles de tres directes. |
|||
| Repartir una quantitat Q en parts directament proporcionals a tres, o més, nombres a, b, c, ... vol dir: | |
| • |
dividir Q en tres, o més, parts, x,
y, z, ..., de manera que es compleixi |
| Un procediment per fer-ho consisteix a resoldre diverses regles de tres directes, tantes com nombres a, b, c, etc. n'hi hagi, la qual cosa ens portarà a resoldre la cadena de proporcions següents: | |
| Exemple 3 | |
| Tres amics, el Joaquim, l'Alfred i el Blai, compren en un magatzem de fruites una capsa de 25 Kg de pomes per 70 €. Han posat, respectivament, 30 €, 25 € i 15 € i no disposen de cap balança per pesar el que li tocaria a cada un, però han tingut molta sort, ja que han comptat el nombre total de pomes i els hi han sortit 140. En Joaquim ha proposat deseguida un repartiment que a tots tres els hi ha semblat molt just. Quin pot ser el mètode? | |
Lògicament, el mètode consistirà en repartir 140 pomes en parts directament propocionals a les quantitats pagades: 30, 25 i 15. Això els hi portarà a la resolució de les següents proporcions, en les quals x representa el nombre de pomes que li corresponen al Joaquim, y les que li toquen a l'Alfred, i z les que s'ha d'emportar el Blai: |
|
| Així doncs, el Joaquim s'emportarà 60 pomes; l'Alfred, 50, i el Blai, 30. | |
Podeu veure més exemples en la següent escena. |
|
Repartiments inversament proporcionals
Malgrat el més normal a la vida és fer als repartiments directament proporcionals, hi ha situacions en les quals un repartiment d'aquesta clase resultaria inadequat. Per exemple, si ha de donar un premi als concursants que passin una determinada prova i al final resulta que n'hi ha més d'un que la passa, aleshores sembla lògic que rebi una part més grossa aquell que hagi trigat menys temps a realitzar-la. En casos com aquests, se sol considerar normal fer el repartiment de manera inversament proporcional al temps invertit.
Més exactament:
| Repartir una quantitat Q en parts inversament proporcionals a tres, o més, nombres a, b, c, ... vol dir: | |
| • |
dividir Q en tres, o més, parts, x, y, z, ..., que siguin directament proporcionals als inversos de a, b, c, .., és a dir, |
|
de manera que es compleixi 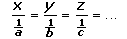 |
|
| El procediment per fer-ho consistirà, doncs, en resoldre el següent sistema de proporcions (on Q és la quantitat a repartir): | |
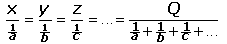 |
|
Com podeu veure, perquè sapigueu fer repartiments inversament proporcionals, heu d'aprendre abans alguna forma de sumar fraccions. És per això que, malgrat les operacions amb fraccions corresponen a un altre crèdit, explicarem el concepte de suma de fraccions i, si més no, un mètode general per fer sumes.
Suma de fraccions amb denominadors iguals
Com podeu observar en la figura de la dreta, |
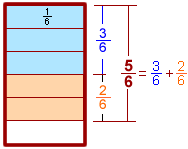 |
||
| • | Per sumar fraccions que tenen iguals els denominadors, se sumen els numeradors i es deixa el mateix denominador que tenien les fraccions sumades. | ||
| Així doncs, quan els denominadors són iguals, la suma de fraccions es fa igual que la suma de enters: | |||
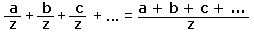 |
|||
| Exemples | |||
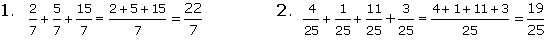 |
|||
Suma de fraccions amb denominadors NO iguals
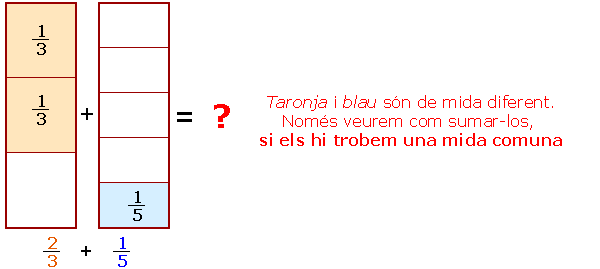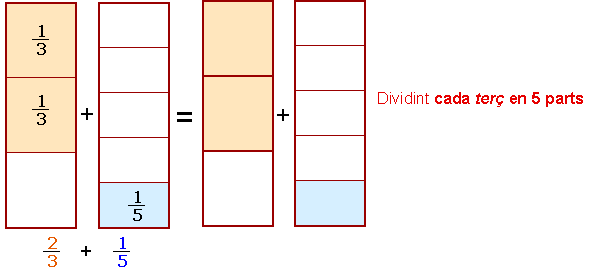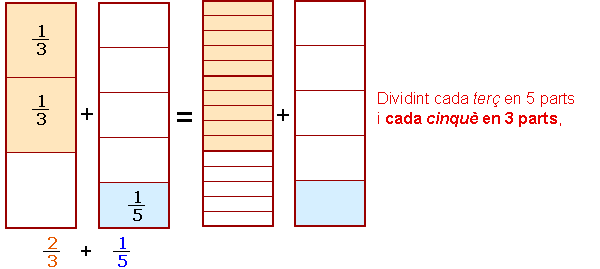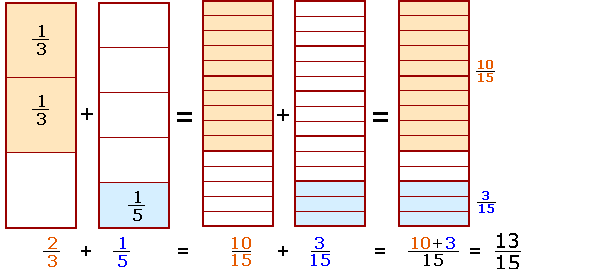
La següent animació us ajudarà a entendre més fàcilment la fórmula posterior de suma de fraccions amb denominadors desiguals. (Si no veieu l'animació, activeu l'opció veure animacions en el vostre navegador (En Internet explorer: Herramientas / Opciones de internet / Opciones avanzadas /Multimedia /Activar animación en páginas web).) |
||
 |
||
| Si heu parat prou l'atenció a la forma de sumar, us haureu adonat que, per obtenir la suma de les dues fraccions, | ||
|
1. |
S'ha pres com a denominador comú el producte dels dos denominadors (5·3 = 15) | |
|
2. |
S'ha multiplicat el numerador de cada fracció pel denominador de l'altra, s'han sumat aquests resultats i s'ha posat com a numerador final (2·5+1·3 = 13) | |
I aquest mateix mètode és el que podreu utilitzar per sumar dos o més fraccions:
| Per sumar dos o més fraccions, | |
1. |
Com a denominador del resultat es pot prendre el producte dels denominadors de les fraccions que se sumen. Aleshores, |
2. |
es multiplica el numerador de cada fracció pels denominadors de les altres fraccions i se sumen els resultats obtinguts i, finalment, |
| 3. |
com a numerador del resultat, s'agafa la suma obtinguda a l'apartat 2. |
| En resum, es tracta d'aplicar la fórmula següent | |
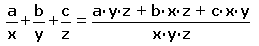 |
|
| Exemple 4 | |
|
• |
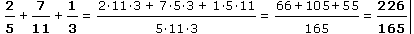 |
• |
|
Podeu veure més exemples en la següent escena.
|
|
Altres operacions
No entrarem en detalls; només heu de saber la següent fórmula, de multiplicació d'un nombre per una fracció. (En realitat, si el nombre és enter, la fórmula és una conseqüència molt senzilla de la forma de sumar fraccions amb denominadors iguals.)
| és a dir, per multiplicar un nombre per una fracció, es multiplica el nombre pel numerador i es deixa el mateix denominador que tingui la fracció. |
| Exemple 5 |
• Una forma ràpida de calcular el producte • Altre forma d'arribar al mateix resultat consistiria en sumar
3 vegades la fracció; així: |
Una aplicació dels repartiments proporcionals: Problemes de mescles
Sovint, certs fabricants han de fer mescles d'un producte de diferents qualitats i preus per tal d'obtenir un producte final que agradi més al consumidor. Qui no ha vist, per exemple, als supermercats "café amb una part de café natural i altre part de torrefacte"? Qui no ha vist ampolles de vi que contenen realment vins de diferents classes (una part de merlot i altre cabernet sauvingon, ...) Qui no sap que un objecte d'or no sol ser d'or pur, és a dir, que conté una part que és d'un altre metall?
La regla que resol els problemes derivats de les mescles es diu regla d'al·ligació. No n'aprofundirem massa, però resoldrem un parell de situacions simples, que resulten en realitat conseqüència immediata d'aplicar repartiments directament proporcionals
Exemples
| 1. | Problema
directe: Un fabricant de café mescla 1200 Kg
de café natural, de 7 € el Kg, amb 800 Kg
de torrefacte de 3 € el Kg. Quin hauria de ser el
preu just de la mescla? |
|
Els problemes d'aquest tipus se solen conèixer amb el nom d'al·ligació directa. S'hauran de resoldre trobant un preu mitjà, x, entre 7€ i 3€ el Kg, de tal manera que allò que es perdi en vendre el café a menys de 7€ es guanyi en vendre l'altre part a més de 3 € el Kg. Organitzem primer les dades reflectint la pèrdua o benefici sobre cada café (fixeu-vos bé en l'animació): |
||
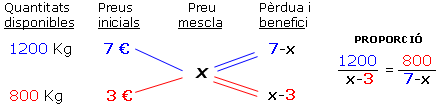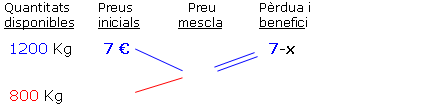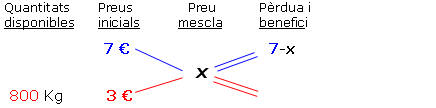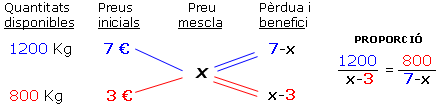 |
(A) | |
| Aleshores, perquè el preu mitjà sigui just, 1200 i 800 haurien de ser repartits de manera directament proporcional al benefici (x-3) i a la pèrdua (7-x), és a dir, s'hauria de complir | ||
| (B) | ||
| D'aquesta proporció, que podeu resoldre si recordeu la propietat fonamental de les proporcions (producte dels extrems = producte del mitjans), es dedueix x = 5'4 €. (Si us resulta difícil resoldre la proporció, també podeu raonar calculant el preu de cost i el preu de la mescla: | ||
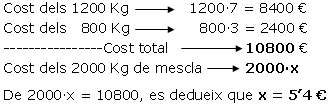 |
(C) | |
| 2. | Problema invers: Quants Kg de café de 7 €/Kg i quants de café de 3 €/Kg hem de mesclar per obtenir 2000 Kg de café el preu del qual sigui de 4 €/Kg? | |
Els problemes de mescles enunciats d'aquesta manera (és a dir, es coneixen tots els preus i una quantitat i s'han d'esbrinar les altres quantitats) se solen anomenar d'al·ligació inversa. La veritat és que si s'organitzen les dades com hem fet en l'esquema (A), aleshores la resolució és molt senzilla plantejant una proporció tal com la (B). Fem-ho: |
||
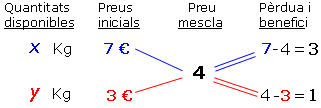 |
(A') | |
|
Com en la proporció (B), les quantitats
x i y han de ser
proporcionals al benefici i a la pèrdua, és a dir, s'ha
de complir |
||
| (B') | ||
| Aquesta proporció la podem resoldre fàcilment si utilitzem la segona propietat bàsica de les proporcions (la recordeu?... quinzena 2), segons la qual obtindrem una fracció equivalent a aquestes dues si sumem d'una banda els numeradors i, d'altra, els denominadors, és a dir, | ||
Com que la suma de les quantitats x
i y ha de coincidir amb la quantiat total de
mescla (2000 Kg), obtenim 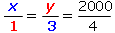 .
Per tant, .
Per tant, |
||
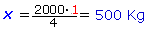 |
||