a) operació interna :    E x E  -----> E     que representarem per +

b) operació externa    k x E -------> E    que representarem per *

Aquestes operacions compleixen les següents propietats:

1. (a+b) +c = a+(b+c)           associativa
2. a+0 = 0+a = a                   0 element neutre de la suma
3. a+(-a) = (-a) + a = 0          element oposat
4. a + b = b + a                     commutativa
5. (x + y )*a = x*a +y*a
6. x*(a+b) = x*a + x*b            distributiva
7. (x*y)*a = x*(y*a)                 associativa del producte
8. 1* a = a                             1 element neutre del producte

a,b,c (anomenats vectors) pertanyen a E i x,y (escalars) pertanyen a k

Exemples de espais vectorials sobre el cos dels reals poden ser el pla (RxR), l'espai (RxRxR) però també altres conjunts molt allunyats de la nostra intuïció de "espai", com els polinomis d'una variable sobre els racionals, o el conjunt dels complexes sobre el cos dels reals)

Números complexos: conjunt numèric que inclueix els números reals, però que permet, a més, fer la radicació de números negatius. Els números complexos tenen la forma:

                  a + b i   amb a i b números reals i el número i arrel quadrada de -1.

Cada número complex es pot representar com un punt en un pla cartesià de coordenades (a, b).

Per entendre la generació dels conjunts de Julia i Mandelbrot, només necessitem conèixer la suma i multiplicació de complexos, i adonar nos que i . i = -1.

   suma  ( a+b i) + (c + d i) =   (a+c) + (b+d) i

   multiplicació    ( a+b i) . (c + d i) = ab + ad i + bc i + bd  i.i = (ab - bd) + (ad + bc) i

Translació: És una transformació geomètrica que "mou" les figures sense canviar la seva forma. Donat un vector v, la translació transforma un punt A en un punt B de forma que  B= A+ v

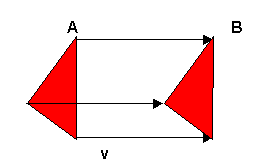
La expressió matricial de la equació anterior, considerant les minúscules com a les components dels punts i del vector quedaria de la forma següent (en el pla)

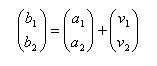
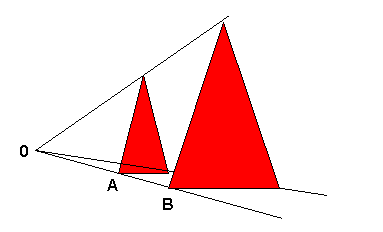
Homotècia: La homotècia transforma les figures geomètriques en altres semblants (proporcionals). Més tècnicament, donat on punt O i un nombre real K, la homotècia fa correspondre a un punt A un altre B, alineat amb A i O de manera que: d(OA)=Kd(OB)

Podem pensar sempre que el punt o coincideix amb el A, i que tot seguit realitzem una translació. La expressió matricial quedaria en aquest cas:

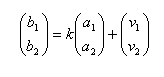
Rotació : Una rotació o gir de centre O i angle a transforma un punt A del pla en un altre B mitjançant una rotació d'angle a.

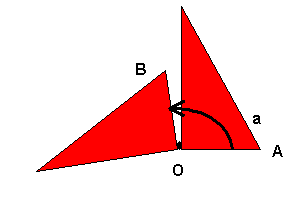
Si O es l'origen de coordenades, el gir es descriu matricialment amb la forma:

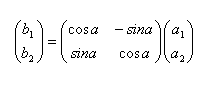
Diagrama de fases: Es un gràfic cartesià on es representen les variables x(t) i v(t) d'un sistema dinàmic (que evoluciona amb el temps). Aquests diagrames son especialment útils per sistemes periòdics. Per exemple, en un pèndul ideal que oscil·lés eternament, el diagrama de fases seria una elipse:

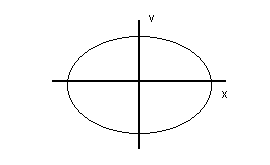
En un pèndul real, que per dissipació acabaria aturant-se, la elipse degeneraria en una espiral, fins acabar en el (0,0).

Efecte papallona: . "El vol d'una papallona al Japó pot provocar un huracà al Carib". Aquesta frase es el origen de la expressió efecte papallona. Significa que, per alguns sistemes, petites diferencies en el input poden provocar efectes molt intensos, (grans diferencies en el output) i a vegades indesitjables, en els sistemes dinàmics caòtics.