(2024-juny-1-1) Considereu la funció `f(x) = 2ln(x)/x` , definida per a `x > 0`. a) Estudieu-ne els màxims i els mínims, i les zones de creixement i de decreixement. [1 punt] b) Aquesta funció té asímptotes? Feu un esbós de la seva gràfica. [1 punt] c) Calculeu l’equació de la recta tangent a la gràfica de `y = f(x)` en el punt d’abscissa `x = 1`. [0,5 punts] Solució: a) Per trobar els màxims, mínims i intervals de creixement o decreixement ho podem fer a partir de la funció derivada: `f'(x)=2(1/x·x-ln(x)·1)/x^2=2(1-ln(x))/x^2` Per trobar candidats a extrems relatius (màxims o mínims) podem igualar a `0` l'anterior expressió, que només ho pot ser quan el numerador val `0`. `1-ln(x)=0 =>ln(x)=1 => x=e` Per veure si és un mínim o un màxim anem a recordar quina forma té la funció `ln(x)`. També ens serà útil per contesrar altres preguntes que ens demanen. Això es podria fer d'una altra manera, calculant la segona derivada, per exemple. La funció `ln(x)` per nombres més petits que `e`, son uns nombres més petits que `1` la qual cosa fa que a l'esquerra d'`e` la funció derivada: `f'(x)=2(1-ln(x))/x^2=2(1-0'...)/x^2>0` Per la qual cosa a l'esquerra d'`e` la funció derivada és positiva per la qual cosa `f(x)` és creixent per a `x < e` La funció `ln(x)` per nombres més grans que `e`, son uns nombres més grans que `1` la qual cosa fa que a la dreta d'`e` la funció derivada: `f'(x)=2(1-ln(x))/x^2=2(1-1'...)/x^2<0` Per la qual cosa a dreta d'`e` la funció derivada és negativa per la qual cosa `f(x)` és decreixent per a `x>e` Tot plegat implica que en un punt,`x=e`, on la derivada val `0`, i la funció és creixent a l'esquerra i decreixent a la dreta, hi ha un màxim. `f(e)=2ln(e)/e=2/e => (e,2/e)` hi ha un màxim. El domini de `f(x)` és `(0, +infty)` ja que el `ln(x)` només està definit en aquest interval. I pel que hem dit abans de quant la derivada era positiva i negativa implica que: `f(x)` és creixent a `(0,e)` i decreixent a `(e, +infty)=` b) Per fer un esboç de la funció calcularem els punt de tall amb l'eix `x` i les asímptotes en cas de que en tingui. Punts de tall eix `x`: `2ln(x)/x=0` `ln(x)=0` `x=1` Calculem `\lim_{x\to 0^+} 2ln(x)/x= -infty/0=-infty` això implica que a `x=0` hi ha una asímptota vertical `x=0` Per mirar si hi ha una asímptota horitzontal, cal calcular límit quan `x` tendeix a `+infty` `\lim_{x\to +infty}2ln(x)/x=(+infty)/(+infty)` indeterminat i podem calcular-lo amb la regla de l'Hopital: `\lim_{x\to +infty}2ln(x)/x=\lim_{x\to +infty}2(1/x)/x=\lim_{x\to +infty}2/x^2= 0`. O sigui,sí que hi ha una asímptota horitzontal `y=0`. Amb tot això procedim a der l'esboç. 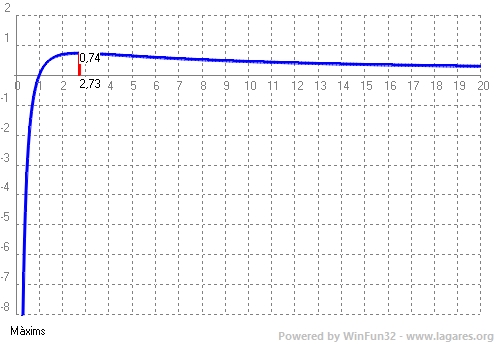No hem calculat el punt d'inflexió que el podríem trobar si igualessim la segona derivada a `0`. c) Per trobar l'equació de la recta tangent en el punt `x=1` només cal calcular la imatge `f(x)=2ln(1)/1=0` i el pendent de la recta que el podem trobar substituin a la derivada: `f'(x)=2(1-ln(x))/x^2 => m=f'(1)=2(1-ln(1))/1^2=2` Fent servir l'equació punt pendent, `y-y_0=m(x-x_0)` l'equqció de la recta tangent demanada queda: `y-0=2(x-1)` `y=2x-2` L'exercici no ho demana, però podem veure quin seria el dibuix de la funció ambaquesta recta tangent: