La integral definida


Exercicis:


1- Calcula, tant per excès, com per defecte, l'àrea entre `x=0`, `x=4`, la funció, `x^2` i l'eix de les `x` fent servir `\Delta x = 0'5`. Quant val `n` en aquest cas?.


    `0'5·(0^2+0'5^2+1^2+1'5^2+2^2+2'5^2+3^2+3'5^2)=17'5`


    `0'5·(0'5^2+1^2+1'5^2+2^2+2'5^2+3^2+3'5^2+4^2)=25'5`


2- Calcula, tant per excès, com per defecte, l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x` fent servir `\Delta x = 1`. Quant val `n` en aquest cas?.


    `1·(0+1+2+3+4+5+6+7+8+9)=45`


    `1·(1+2+3+4+5+6+7+8+9+10)=55`


3- Calcula l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x`, fent servir propietats geomètriques del dibuix de la gràfica resultant.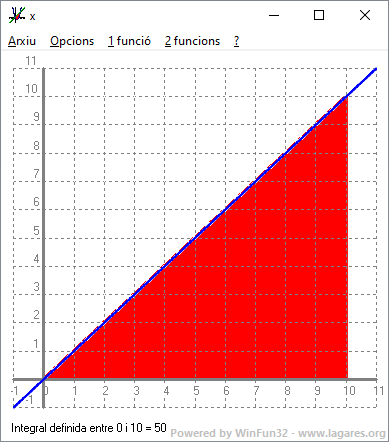



    Àrea = `(10·10)/2=50`


4- Calcula l'àrea entre `x=0`, `x=10`, la funció, `x` i l'eix de les `x`, calculant el `lim_(n->+\infty) \sum_(i=1)^n x_i·\Delta x`.


    `lim_(n->+\infty) \sum_(i=1)^n x_i·\Delta x`


    `x_i=i/n`


    `\Delta x = 10/n`


    `lim_(n->+\infty) 10/n·\sum_(i=1)^n i/n`


    `n=10 => 10/10·(1+2+3+4+5+6+7+8+9+10)`


    `n=20 => 10/20·(0'5+1+1'5+2+2'5+...+8'5+9+9'5+10)`


    Els números de la suma segueixen una progressió aritmètica, cada terme és l'anterior més una constant, en aquest cas `0'5`. En una progeressió aritmàtica es pot veure que la suma és la meitat de sumarla dues vegades:


    `S_n=((A_1+A_n)·n)/2`


    `10/20·((0'5+1+1'5+2+2'5+...+8'5+9+9'5+10)+(10+9'5+9+8'5+...2'5+2+1'5+1+0'5))/2=`


    `10/20·((0'5+10)+(1+9'5)+(1'5+9)+...+(9+1'5)+(9'5+1)+(10+0'5))/2=`


    `10/20·(10'5·20)/2=52'5`


    En general:


    `lim_(n->+\infty) 10/n·\sum_(i=1)^n i/n = lim_(n->+\infty) (10/n·(1/n+10)/2·n)= lim_(n->+\infty) (10(1/n+10)/2)= lim_(n->+\infty) (10/(2n)+100/2)=50`