|
2-(2019-juny-1-4) Considereu la funció `f(x)=(2x^3-5x+4)/(1-x)`. a) Calculeu-ne el domini i estudieu-ne la continuïtat. Té cap asímptota vertical? b) Observeu que , `f(0) = 4` i `f(2) = -10`. Raoneu si, a partir d'aquesta informació, podem deduir que l'interval `(-2, 0)` conté un zero de la funció. Podem deduir-ho per a l'interval `(0, 2)`? Trobeu un interval determinat per dos enters consecutius que contingui, com a mínim, un zero d'aquesta funció. a) És un quocient de polinomis el domini són tots els Reals excepte on el denomunador sigui `0` i això passa per `x=1`. La qual cosa `=>` que la funció és contínua per tots els `x` del seu domini (`R-{1}`) `\lim_{x\to 1}(2x^3-5x+4)/(1-x)=1/0=\infty =>` la funció té una asímptota vertical `x=1` b) No ho podem deduir (Teorema de Bolzano) ja que tot i que les imatges tenen diferent signe com la funció no és contínua a l'interval `(0,2)` `f(-2)=(-16+10+4)/3=(-2)/3 => f(-2)·f(0)<0 =>` Hi ha un zero de la funció a l'interval `(-2,0)` Per trobar un interval determinat per dos enters consecutius el que farem és calcular la imatge de `x=-1` `f(-1)=(-2+5+4)/2=7/2>0`. O sigui el zero es trobarà a l'interval `(-2,-1)` No ho demana l'exercici, però per ajudar a la comprensió aquí teniu el dibuix de la gràfica: 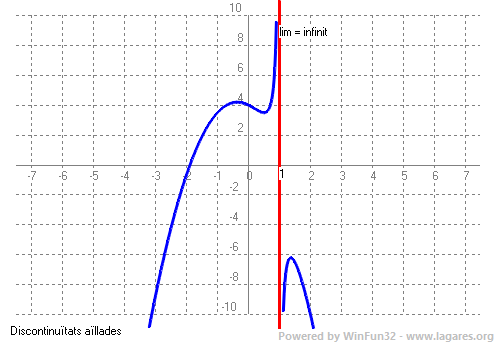 |