|
3-(2019-juny-1-6) Considereu les funcions `f(x) = x^2` i `g(x)=1/x`, i la recta `x = e`. a) Feu un esbˇs de la regiˇ delimitada per les seves grÓfiques i l'eix de les abscisses. Calculeu les coordenades del punt de tall de `y = f(x)` amb `y = g(x)`. b) Calculeu l'Órea de la regiˇ descrita en l'apartat anterior. a) 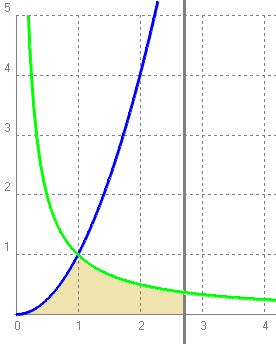 `x^2=1/x => x^3=1 =>x=1 => (1,1)` b) Cal calcular l'Órea entre `0` i `1` fent la integral definida de la funciˇ `x^2` i la integral definida entre `1` i `e` de la funciˇ `1/x`. `\int_0^1x^2dx+\int_1^e1/xdx=[x^3/3]_0^1+[lnx]_1^e=1/3+lne-ln1=1/3+1=4/3 u^2` |