5-(2019-juny-4-4) Considereu la funció f(x), que depèn dels paràmetres reals `n` i `m` i és definida per $$ f(x)=\begin{cases}e^x & si & x\le 0\\\ \frac{x^2}{4}+n & si & 0 < x\le 2\\\ \frac{3x}{2}+m & si & x>2\end{cases} $$ a) Calculeu els valors de `n` i `m` perquè la funció sigui contínua a tot el conjunt dels nombres reals. b) Per al cas `n = -4` i `m = -6`, calculeu l'àrea de la regió limitada per la gràfica de `f(x)`, l'eix de les abscisses i les rectes `x = 0` i `x = 4`. a- Es tracta d'una funció definida a trossos, tres, que cadascuna d'elles es contínua sempre per la qual cosa els únics llocs on podríme tenir una discontinuïtat seria a les fronteres, `0` i `2`. Per la qual cosa el que farem es fer coincidir els límis per l'esquerra i la dreta en ambdos llocs. `\lim_{x\to 0^-} f(x)= e^0=1` i `\lim_{x\to 0^+} f(x)= 0^2/4+n=n => n=1` `\lim_{x\to 2^-} f(x)= 2^2/4+n=1+n`, i: `\lim_{x\to 2^+} f(x)= (3·2)/2+m=3+m => 1+n=3+m => 1+1=3+m => m=-1` b- $$ f(x)=\begin{cases}e^x & si & x\le 0\\\ \frac{x^2}{4}-4 & si & 0 < x\le 2\\\ \frac{3x}{2}-6 & si & x>2\end{cases} $$ Cal calcular la integral definida entre `0` i `2` fent servir la funció `x^2/4-4` i entre `2` i `4` fent servir la funció `(3x)/2-6` Dibuixem la gràfica, una paràbola i un recta, per veure si té punts de tall amb l'eix de les `x`. 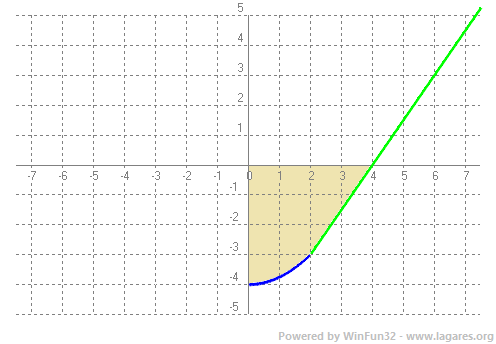`|\int_0^2 (x^2/4-4)dx|= |[x^3/12-4x]_0^2=8/12-8|=2/3-8=22/3` `|\int_2^4 ((3x)/2-6)dx =[(3x^2)/4-6x]_2^4|=|(12-24)-(3-12)|=3` Àrea total `=22/3+3=31/3` `u^2`