9-(2019-setembre-5-6) Considereu la funció `f(x)=ln(x)/x`. a) Calculeu el domini de la funció `f`, els punts de tall de la gràfica de `f` amb els eixos de coordenades, i els intervals de creixement i decreixement de `f`. b) Calculeu l'àrea de la regió del pla determinada per la gràfica de la funció `f`, les rectes `x = 1` i `x = e`, i l'eix de les abscisses. a- Domini el `ln(x)` només està definit per `x>0`. O sigui domini `(0,+\infty)` Talls eix `x` `ln(x)/x=0 => ln(x)=0 => x=1` Talls eix `y` no en té, ja que no hi ha `f(0)` Per trobar els intervals de creixement i de decreixement cal calcular la derivada i veure on és `+` o `-`. `f'(x)=(1/x·x-ln(x)·1)/x^2=(1-ln(x))/x^2=0 => 1-ln(x)=0 => ln(x)=1 => x=e` Calculem els signe de `f'(x)` a l'esquerra de `e` `f'(1)=(1-ln(1))/1^2=1>0` vol dir que és creixent `(0,e)` I el signe de `f'(x)` a la dreta de `e` `f'(e^2)=(1-ln(e^2))/1^2=(1-2)/1=-1<0` vol dir que és decreixent `(e,+\infty)` b- `\int (ln(x)/x)dx=\int tdt=t^2/2+c=ln^2(x)/2+c` `ln(x)=t => 1/x=dt` `\int_1^e (ln(x)/x)dx=[ln^2(x)/2]_1^e=1/2-0=1/2` `u^2` El problema no ho demana, però la gràfica i l'àrea calculada és: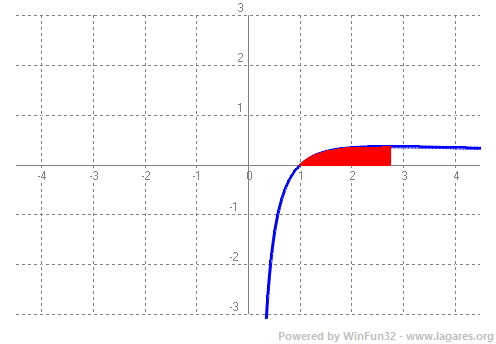