|
18-(2020-setembre-4-5) Una empresa estÓ treballant en el disseny d'unes cÓpsules de cafŔ. L'empresa ha constru´t la secciˇ transversal de les cÓpsules inscrivint-la en una semicircumferŔncia de radi `1`, trašant a continuaciˇ una corda `CD` paralĚlela al diÓmetre `AB` i incorporant el punt `E` en el punt mitjÓ de l'arc `CD`. D'aquesta manera queda trašat el pentÓgon `ACEDB`, tal com es mostra en la figura. 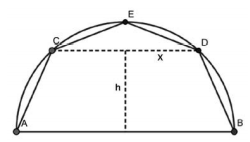 a) Expresseu en funciˇ de `x` i `h` l'Órea del pentÓgon `ACEDB`. b) Quina ha de ser la distÓncia (indicada en la figura per `h`) a quŔ s'ha de situar la corda `CD` de `AB` per tal que l'Órea del pentÓgon `ACEDB` sigui mÓxima? a) L'Órea del pentÓgon la podem descriure com l'aprea d'un trapezi mÚs l'Órea d'un triangle. └rea triangle `= (\text{base} \times \text{altura})/2` on la `\text{base}=2x` i l'`\text{altura}= \text{radi}-h` Ja que `\text{radi}=1` Ja que la base gran mesura `2` radis i la base petita `2x` L'Órea del pentÓgon: b) Per trobar la distÓncia `h` que fa que l'Órea sigui mÓxima hem de posar `x=f(h)` i ho podem fer ja que tenim un triangle rectangle amb catets `x`, `h` i hipotenusa `1 => x=sqrt(1-h^2)` el que fa que podem expressar l'Órea del pentÓgon: Si ho derivem:
Ho igualem a `0`
Per demostrar que Ús un mÓxim podem calcular l'Órea per aquest valor: `A(sqrt(2)/2)=sqrt(1-2/4)+sqrt(2)/2=sqrt(1/2)+sqrt(2)/2=sqrt(2)`. I si cerquem valors a la seva esquerra i a la dreta, `A(0)=1` i `A(1)=1` que clÓrament sˇn mÚs petits que `sqrt(2)` |