|
(2022-setembre-3-6)- La imatge següent mostra dues parets perpendiculars d’una sala representades en uns eixos de coordenades, de manera que una paret és al pla `y = 0` i l’altra és al pla `x = 0`. 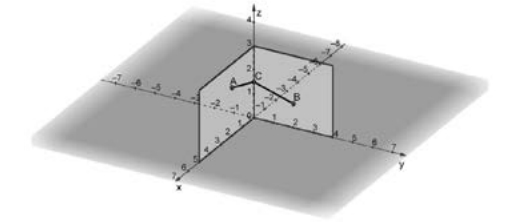 En el punt `A=(2,0,2)` hi volem penjar un altaveu que ha d'estar connectat a un equip de so, el qual està situat a l'altra paret, en el punt `B=(0,2,1)`. La connexió entre `A` i `B` la farem mitjançant un cable que passi pel punt `C=(0,0,h)`, situat a la recta vertical d'intersecció de les dues parets. Com la qualitat del so de pèn, entre altres actors, de la longitud del cable que uneix els dos aparells, volem fer una instal·lació amb el mínimcable possible. a) Comproveu que la longitud total del cable necessari, en funció d el'latura `h` per on ha de passar el cable a l'eix vertical `OZ`, ve donada per l'expressió `L(h)=\sqrt{h^2-4h+8}+\sqrt{h^2-2h+5}` b) Calculeu les coordenades del punt `C` per on ha de passar el cable per tal que la longitud del cable sigui mínima. Calculeu aquesta longitud mínima del cable. [1,75 punts] SOLUCIÓ:
`\sqrt{4+0+h^2-4h+4}+\sqrt{0+4+h^2-2h+1}=\sqrt{h^2-4h+8}+\sqrt{h^2-2h+5}=L(h)`
`(2h-4)/(2\sqrt{h^2-4h+8})=-(2h-2)/(2\sqrt{h^2-2h+5})` `(h-2)/\sqrt{h^2-4h+8}=-(h-1)/\sqrt{h^2-2h+5}` `((h-2)/\sqrt{h^2-4h+8})^2=(-(h-1)/\sqrt{h^2-2h+5})^2` `(h^2-4h+4)/(h^2-4h+8)=(h^2-2h+1)/(h^2-2h+5)` `(h^2-4h+4)·(h^2-2h+5)=(h^2-2h+1)·(h^2-4h+8)` `h^4-2h^3+5h^2-4h^3+8h^2-20h+4h^2-8h+20=h^4-4h^3+8h^2-2h^3+8h^2-16h+h^2-4h+8` `8h=12 => h=12/8=3/2=1,5` Per comprovar que és un mínim podem calcular el valor de la derivada abans i després d'`1,5` `L'(1)=(2·1-4)/(2\sqrt{1^2-4·1+8})+(2·1-2)/(2\sqrt{1^2-2·1+5})=(-2)/(2\sqrt{5})+(0)/(2\sqrt{4})=-1/\sqrt{5}<0` `L'(2)=(2·2-4)/(2\sqrt{2^2-4·2+8})+(2·2-2)/(2\sqrt{2^2-2·2+5})= 0/(2\sqrt{4})+(2)/(2\sqrt{5})=1/\sqrt{5}>0` A l'esquerra de `3/5` la derivada és negativa i a la dreta, positiva `=>` a `x=3/5` hi ha un mínim. |