Calculeu els coeficients `a`, `b`, `c` i `d` de la funció `f(x) = ax^3 + bx^2 + cx + d` si sabem que l’equa- ció de la recta tangent a la gràfica de la funció `f` en el punt d’inflexió `(1, 0)` és `y = –3x + 3` i que la funció té un extrem relatiu en el punt de la gràfica d’abscissa `x = 0`. [2,5 punts] Solució: Si `f(x)` té un punt d'inflexió en el punt `(1,0)` vol dir dues coses: `f(1)=0 => a·1^3+b·1^2+c·1+d=0 => a+b+c+d=0` `f''(1)=0 => f'(x)=3ax^2+2bx+c => f''(x)=6ax+2b => f''(1)=6a+2b=0` Si en el punt d'inflexió, `(1,0)` la recta tangent és `y=-3x+3` vol dir que la derivada de `f(x)` en `x=1` val `-3 =>` `f'(1)=3a+2b+c=-3` Sí la funció té un extrem relatiu en el punt d'abscissa `x=0 =>` que la derivada en aquest punt val `0`. `f'(0)=c=0` Tenim un sistema de `4` equacions amb `4` incògnites, de fet de `3` equacions amb `3` incògnites, ja que `c=0`. Si el podem resoldre tindrem la solució al nostre problema, el coeficients de la funció: $$ \begin{cases} a+b+d=0\\ 6a+2b=0\\ 3a+2b=-3 \end{cases} $$ I descobrim que encara és més senzill ja que les dues últimes equacions formen un sistema de `2` equacions amb `2` incògnites. El resoldrem i a partir de la primera equació podrem trobar la `d` que és la incògnita que ens faltarà. $$ \begin{cases} 6a+2b=0\\ 3a+2b=-3 \end{cases} $$ Fem una reducció multiplicant per `-2` la segona equació: $$ \begin{cases} 6a+2b=0\\ -6a-4b=6 \end{cases} $$ Ho sumem i ens queda: `-2b=6 => b=-3` Ho podem substituir a la primera equació `6a+2·(-3)=0 => 6a-6=0 => 6a=6 => a=1` Substituim `a=1` i `b=-3` a la primera equació `a+b+d=0 => 1-3+d=0 => d=2` Finalment queda la solució del problema `(a=1, b=-3, c=0, d=2)`: `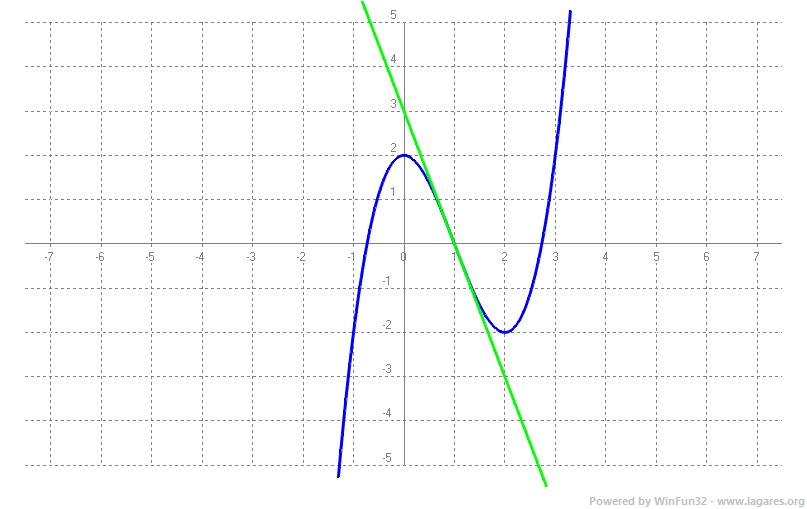f(x)=x^3-3x^2+2` ANNEX: Si dibuixem la gràfica i la recta veiem que realment la recta que passa pel punt d'inflexió, `(1,0)` és la que ens diuen `y=-3x+3` y la funció té un extem en `x=0`, concretament un màxim .