Sigui la funció derivada d’una funció derivable` f(x)` que passa pel punt `A = (0, 3)`. $$ f'(x)=\begin{cases} x-1 \text{, si } x\le2\\ \\ \frac{1}{x-1} \text{, si } x>2\end{cases} $$ a) Calculeu la funció `f(x)`. [1,5 punts] Solució: Cal que integrem les dues funcions `\int (x-1) dx = x^2/2-x+C` i `\int1/(x-1) dx = ln(x-1)+C'` Com passa per `(0,3)` i `0 <=2 =>` que per calcular `f(0)` cal fer servir la primera funció i ens peremtrà trobar el valor de `C`. `f(0)=0^2/2-0+C=3 => C=3` Amb això tenim la funció definida: $$ f(x)=\begin{cases} \frac{x^2}{2}-x+3 \text{, si } x\le2\\ \\ ln(x-1)+C' \text{, si } x>2\end{cases} $$ Per trobar `C'` farem servir que la funció cal que sigui contínua en `x=2` (ja que ens han dit que és derivable) per la qual cosa cal que calculem el límit per la dreta i el límit per l'esquerra quan tendim a `2` i fer que siguin iguals. `\lim_{x\to 2^-} f(x) =\lim_{x\to 2^+} f(x) =>` `\lim_{x\to 2^-} [x^2/2-x+3] =\lim_{x\to 2^+} [ln(x-1)+C'] =>` `2^2/2-2+3 = ln(2-1)+C' =>` `2-2+3 =ln(1)+C' =>` `3 =0+C' => C' = 3` Amb tot això tenim que la funció és: $$ f(x)=\begin{cases} \frac{x^2}{2}-x+3 \text{, si } x\le2\\ \\ ln(x-1)+3 \text{, si } x>2\end{cases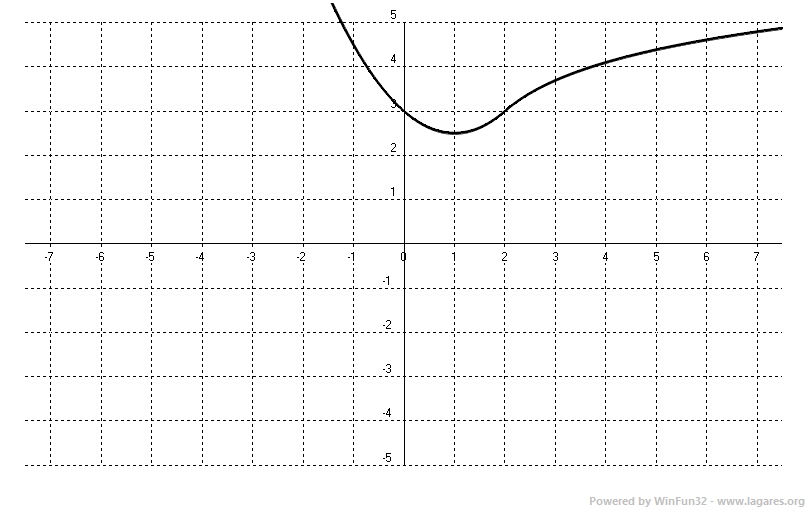} $$ Falta demostrar que la funció és realment derivable. `x^2/2-x+3` és un polinomi és continu i derivable en tots els punts del seu domini. `ln(x-1)+3` és contínua i derivable en tots els punts del seu domini. Hi ha problemes en `x<=1` ja que la funció no està definida en els reals. Donaria `ln(0)` o logaritmes neperians de nombre negatius, però això no dona cap problema ja que la nostr funció definida a trossos fa servir el logaritme neperia quan `x>2`. L'únic lloc on hi podria haver un problema és en la frontera de la funció definida a trossos, `x=2`. Ja sabem que és contínua, hem posat aquesta condició per trobar `C'`. Però és derivable?. Hem de calcular els límits per la dreta i l'esquerra de `f'(x)` en `x=2`. $$ f'(x)=\begin{cases} x-1 \text{, si } x\le2\\ \\ \frac{1}{x-1} \text{, si } x>2\end{cases} $$ `\lim_{x\to 2^-} f'(x) =\lim_{x\to 2^+} f'(x) =>` `\lim_{x\to 2^-} x-1 =\lim_{x\to 2^+} 1/(x-1) =>` `2-1 =1/(2-1) =>` `1 =1/1` Com volíem demostrar ANNEX: Tot i no ser obligatori us mostrem la gràfica de la funció per veure quina forma té i com és contínua i derivable: b-Calculeu l’equació de la recta tangent a la funció `f'(x)` en el punt d’abscissa `x = 3`. [1 punt] Solució: En primer lloc recordem que `3>2` per la qual cosa `f(x)=ln(x-1)+3` i `f'(x)=1/(x-1)` I el que ens demanen és l'equació d ela recta tangent de `f'(x)` o sigui cal calcular `f''(x)= (-1)/(x-1)^2` Per trobar l'equació de la recta tangent, cal un punt `f'(3)=1/(3-1)=1/2 => (3,1/2)` i el pendent: `f''(3)=(-1)/(3-1)^2=(-1)/4` Per trobar l'equació de la recta tangent podem fer servir, per exemple, l'equació punt-pendent: `y-y_0 = m(x-x_0)` Que en el nostre cas és: `y-1/2=-1/4(x-3)` Si volem l'equació explícita: `y=-1/4x+3/4+1/2` `y=-1/4x+5/4`