|
Sigui la funció `f(x)` definida per `f(x) = –3x + e^(2x^(3)-1)`. a) Justifiqueu que `f(x) = 2` té una solució en l’interval `(–1, 0)`. [1,25 punts] Solució:
Anem a veure quins valors agafa aquesta funció en els extrems de l'interval:
`g(0)=-3·0+e^(-1)=e^(-1)>0` Com `g(x)` és una funció contínua (ja que és suma de funcions contínues) i en els extrems d'un interval la funció agafa signes diferents, pel teorema de Bolzano, en aquest interval la funció ha de tenir, com a mínim, un `0 => f(x)=2` té com a mínim una solució. b) Sigui la funció `h(x) = –3x^2 + e^(2x^(3)–1)`. Calculeu l’àrea de la regió compresa entre les gràfiques de les funcions `f(x)` i `h(x)`. [1,25 punts] Solució:
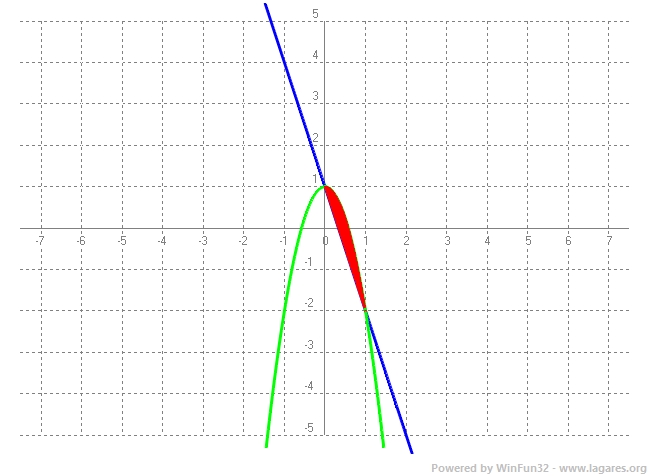
`-3x=-3x^2` `3x^2-3x=0` `3x(x-1)=0` Dues solucions `x=0` i `x=1` Per trobar l'àrea compresa entre les dues funcions cal trobar la integral definida entre els dos punts de tall de la funció diferència de les dues funcions. Si el resultat ens dona negatiu vol dir que hem restat l'inferior menys la superior i cal dir que l'àrea és el valor absolut.
Àrea `=|\int_0^1 (3x^2-3x) dx| = |[x^3-3/2x^2]_0^1| = |1^3-3/2·1^2-0| = |1-3/2|= |-1/2|=1/2 u^2` ANNEX:
 |