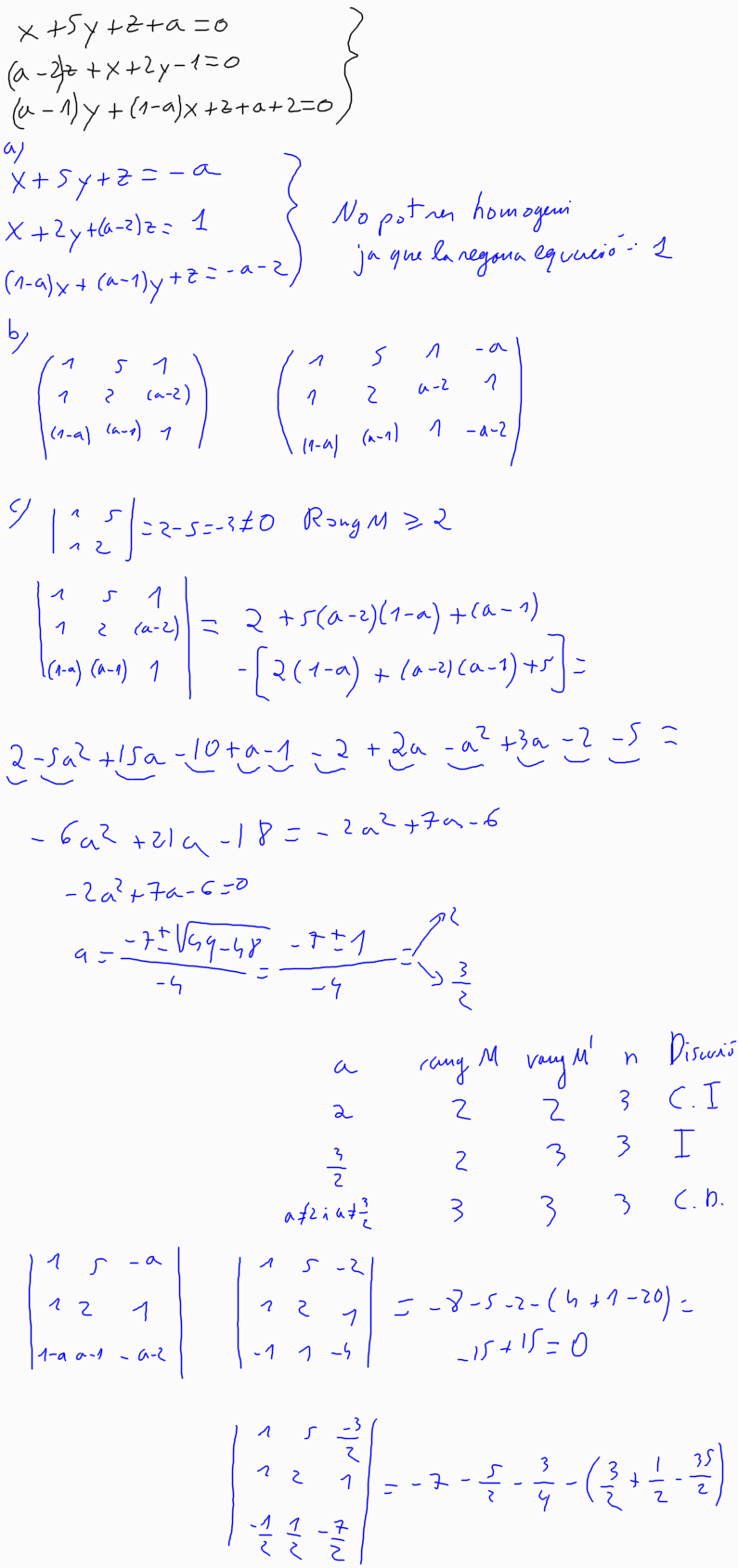Recull d'exercicis de selectivitat. Matrius
3.
(2009-setembre-1) 6. Considereu el sistema d'equacions següent:

a) Expliqueu, raonadament, si es tracta d'un sistema lineal homogeni.
b) Construïu-ne la matriu de coeficients i la matriu ampliada.
c) Trobeu els valors del paràmetre a per als quals el sistema no és
compatible
determinat, i estudieu el caràcter del
sistema en cada un d'aquests casos.
d) Resoleu-lo solament quan el conjunt de les seves solucions és una recta
de  . .
[0,5 punts per l'apartat a; 0,5 punts per l'apartat b; 2
punts per l'apartat c; 1 punt per l'apartat d ]
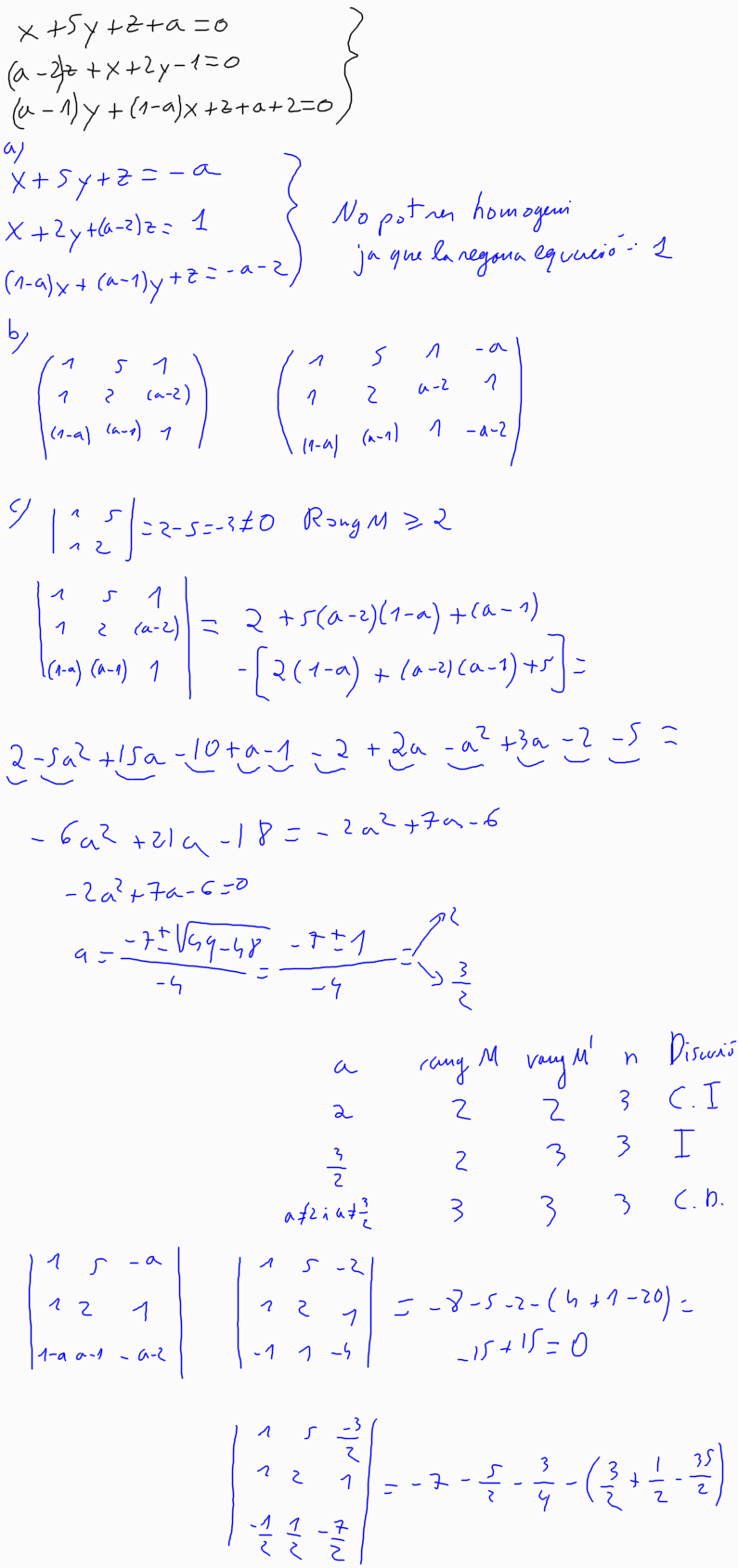
d/
Això és quan el Sistema és Compatibe Indeterminat i això passa quan a = 2
El sistema queda:
x+5y+z+2=0
0z+x+2y-1=0
y-x+z+2+2=0
Si l'arreglem:
x + 5y + z = -2
x + 2y = 1
-x + y + z = -4
Equació inicial:
-x +y +z = -4
+x +2y 0z = +1
+x +5y +z = -2
Canviat l'ordre de les equacions: 1ª, 2ª.
+x +2y 0z = +1
-x +y +z = -4
+x +5y +z = -2
Multipliquem la 1ª equació per 1 i ho sumem a la 2ª equació multiplicada per 1 .
+x +2y 0z = +1
0x +3y +z = -3
+x +5y +z = -2
Multipliquem la 1ª equació per (-1) i ho sumem a la 3ª equació multiplicada per 1 .
+x +2y 0z = +1
0x +3y +z = -3
0x +3y +z = -3
Multipliquem la 2ª equació per (-3) i ho sumem a la 3ª equació multiplicada per 3 .
+x +2y 0z = +1
0x +3y +z = -3
0x 0y 0z = 0
Eliminem la 3ª equació.
+x +2y 0z = +1
0x +3y +z = -3
SISTEMA COMPATIBLE INDETERMINAT.
Passem les incògnites no principals a l'altra banda.
+x +2y = +1 0z
0x +3y = -3 -z
Multipliquem la 2ª equació per (-2) i ho sumem a la 1ª equació multiplicada per 3 .
+3x 0y = +9 +2z
0x +3y = -3 -z
Dividim cada equació pel coeficient de la seva incògnita.
+x 0y = +3 +0.666667z
0x +y = -1 -0.333333z
SISTEMA COMPATIBLE INDETERMINAT.
Solució:
x = +3 +0.666667z
y = -1 -0.333333z
x = +3 +2/3z
y = -1 -1/3z
|