2.1.38-(1995/3/A) Una funció és creixent en tot el seu domini, però la seva derivada és decreixent en tot el domini de la funció. Poseu un exemple de funció que verifiqui aquesta condició i expliqueu el significat d'aquest fet. (2 p)
Calculem la funció deriada:
f(x) = 1/e^x² => f'(x) = -2x / e^x²
Això cal que sigui màxim. Anem a estudiar la gràfica.
Això val 0 per x = 0.
Quan x tendeix a ± infinit tendeix a 0 la derivada.
Si x<0 la derivada és positiva la funció és creixent
Si x>0 la derivada és negativa la funció és decreixent
Tot això ho utilitzem per representar la gràfica:
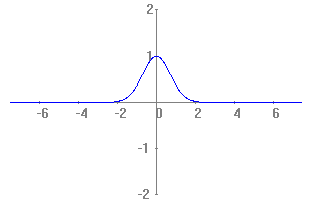
El valor màxim (en valor absolut) l'agafen els punt d'inflexió. Els calcularem:
Calculem f''(x).
f''(x) = [-2e^x² - (-2x)e^x².2x] / (e^x²)² => f''(x) = [2e^x² (-1 +2x²)] / (e^x² )²= 2(-1 +2x²)] / e^x²
f''(x) = 0 (Punts d'inflexió) => -1 +2x² = 0 => x = ± arrel Quadrada de 0,5
x ~ ± 0,7
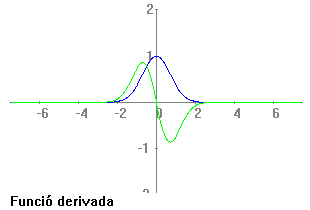
Per ajudar a veure això dibuixem la funció juntament amb la funció derivada