1.Donada la funció f(x) = (x^2-x)/(8x^2+1), es demana que calculeu els límits quan x -> ¥ i quan x -> - ¥, les asímptotes i els punts de tall amb els eixos, i que feu un dibuix aproximat de la seva gràfica. (4 p)
Límit a l'infinit i asímptotes horitzontalsLim x-> (+/-)infinit de la funció és 1/8. És un quocient de polinomis del mateix grau => que la funció té una asímptota horitzontal y = 1/8.
Asímptotes verticals
Per trobar les asímptotes verticals cal trobar prèviament el domini. Al ésser un quocient de polinomis només pot no estar definida quan el denominador és igual a 0.
8x^2+1 = 0 Però això no té cap solució ja que dóna una arrel negativa.
Això fa que el domini sigui tots els reals.
Un quocient de polinomis és continu escepte els punts que no siguin del domini. Ens trobem en un cas que tots els reals són del domini, per lo tant és contínua sempre. O sigui aquesta funció no té asímptotes verticals.
Punts de tall amb l'eix y:
Cal buscar la imatge del 0, f(0) = 0
Punts de tall amb l'eix x:
Cal resoldre la equació formada per la funció igualada a 0.
(x^2-x)/(8x^2+1) = 0
Té dues solucions x =0 i x = 1
Amb tot això no podem acabar de dibuixar la funció, perquè falta trobar els màxims i els mínims.
Màxims i mínims:
Calculem la funció derivada: f(x)' = (8x^2+2x-1)/(8x^2+1)^2
Igualan aquesta funció a 0 tenim els possibles màxims i mínims:
x = -1/2 Substituin trobem la seva imatge y = 1/4
Aquest valor de la y és més gran que el valor de l'asímptota horitzontal (y=1/8) i més gran que el valor de la y en el 0, 0 . Per lo tant en el punt:
(-1/2, 1/4) Hi ha un màxim.
x = 1/4 Substituin trobem la seva imatge y = -1/8
La x d'aquest punt està entre les dues arrels, x=0 i x=1, i la seva imatge és més petita y = -1/8. Tot això fa que en el punt:
(1/4, -1/8) Hi ha un mínim
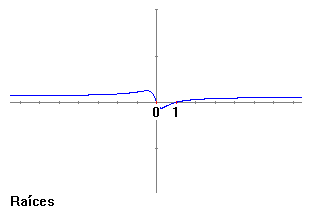
Més o menys el dibuix de la gràfica ha de ser una cosa així: