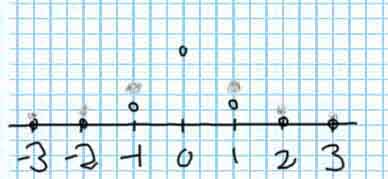
Esta función me la puso en un examen un profesor de cuya madre todavia me acuerdo a veces:
f(x)=1/(3x2-1)2
Esta es una función envenenada, escogida expresamente para que el señor que hace gráficas dibujando los puntos -3, -2, -1, 0, 1, 2 y 3 se equivoque y suspenda.
| x | f(x) |
| -3 | 0,001 |
| -2 | 0,008 |
| -1 | 0,250 |
| 0 | 1,000 |
| 1 | 0,250 |
| 2 | 0,008 |
| 3 | 0,001 |

Lo que significa que nos saldrá otra curva acampanada, sólo que algo más chata, ¿no?
Pues no. En este dibujo podemos ver en rojo la curva acampanada que nos ha salido, y en azul la gráfica de verdad:
Está claro que aquí hay algo que no funciona.
No nos podemos fiar del método de los puntos porque dos de los pasos pueden fallar: el de escoger los puntos (si los escogemos de cualquier manera no sabemos si son los que necesitamos para que la gráfica salga más o menos bien) y el de juntar a ojo con una línea (que muchas veces funciona, pero no siempre).