TEOREMA DEL VALOR MITJÀ

2. TEOREMA DEL VALOR MITJÀ

Si f(x) és una funció continua i definida positiva a l’interval [a,b] existeix un punt c entre a i b tal que:

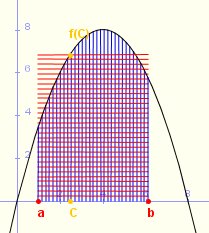
Això es pot interpretar geomètricament: existeix un valor c entre a i b tal que l’àrea del rectangle de base (b-a) i altura f(c) iguala l’àrea del trapezi mixtilini.

Fig2.1,La part ratllada de blau, trapezi mixtilini; part ratllada roig, rectangle.

PRACTICA 2.1.

Obre la finestra de la Wiris i troba "a mà " el valor c que iguala les dues àrees.

EXERCICI 2.1

Calcula l'altura del rectangle de base l'interval [1,3] que iguala l'àrea del trapezi mixtilini determinat per i les rectes x=1 i x=3

Ajuda


pàg ant	inici	pàg seg