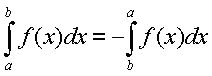1.- Signe de la integral definida:
1.1 Si f(x) és positiva en [a,b] la integral definida és positiva, ja que els valors intermedis que la funció pren en cada un dels intervals de la partició són positius
1.2 Si f(x) és negativa en [a,b] la integral definida és negativa , ja que els valors intermedis que la funció pren en cada un dels intervals de la partició són negatius
1.3 Si f(x) pren valors positius i negatius, la suma total pot ser de qualsevol signe.
2.- Regla de Barrow:
amb F(x) una primitiva de f(x)
3.- Altres propietats:
3.1. Si c ens un punt entre a i b:
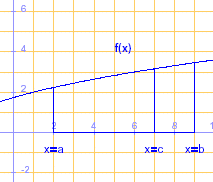 |
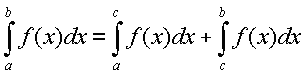 |
3.2 Si a=b el valor de la integral definida és zero
3.3 Si canviem el ordre dels límits canvia de signe la integral
3.4 La integral de la suma (o resta) de funcions es la suma (o resta) d'integrals
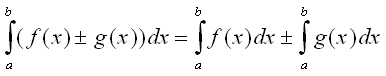
3.5 La integral del producte d'un nombre real per una funció és el producte del nombre per l'integral de la funció

Calcula les següents integrals aplicant la regla de Barrow:
![]()
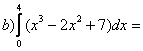
![]()
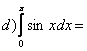


 |
||
|---|---|---|
pàg ant |
inici |
pàg seg |