Mirem imatges
Si observem aquestes imatges ens donen una sensació d'harmonia que, en gran part, procedeix del seu ordre. En el seu esquema bàsic hi ha uns motius que es repeteixen aplicant alguns girs i/o simetries.

També fruïm d'aquestes sensacions observant les imatges que fabrica un calidoscopi.

Pots canviar el gràfic pitjant sobre qualsevol punt del dibuix

Kaleidoscope

(Applet copiat de la pàgina http://gregegan.customer.netspace.net.au/APPLETS/13/13.html)

Els artistes de totes les èpoques coneixen aquest aquesta sensació harmònica que s'obté respectant les simetries i els girs i l'han aplicat a les seves obres.

Partenon (Atenes)

Santa Sofia (Estanbul)

Taj Mahal (Agra)

Notre-Dame (Paris)

Un dels artistes que més va estudiar aquests aspectes va ser el ja esmentat Leonardo da Vinci  que el va dedicar una part del seu temps al problemes de com afegir, sense trencar la simetria, capelles o nínxols a edificis de planta en forma de polígon regular o circular.

Seguirem els seus passos per poder classificar determinats tipus de figures com logos d'empreses, rosasses gòtiques, cúpules, dissenys amb rajoles o de tapaboques de cotxes.

Abans, però haurem d'estudiar la part més teòrica del tema.

 
Moviments isomètrics
Iso en grec vol dir igual i mètric indica que és relatiu a la mesura. Per tant un moviment isomètric aplicat a una figura serà un moviment que no afecti a les mesures; que no augmenti o disminueixi les mides de la figura original.

Hi ha tres moviments isomètrics bàsics.

  • la translació respecte a un vector que ens indica la direcció del desplaçament i la longitud.

  • el gir respecte a un punt i amb un angle donat.

  • la simetria respecte a un eix o a un punt. A l'exemple et proposem una simetria respecte a un eix que és la que estudiarem.
Moviments que superposen
Dintre d'aquests moviments ens interessaran ara els que deixen la figura superposada sobre sí mateixa (invariant), de manera que, un cop aplicat el moviment no notem cap diferència. Per tant haurem de descartar les translacions que no permeten aquestes superposicions. Ens centrarem en els girs i simetries.

Una figura sempre admet un gir de 360º que la "deixa com estava".

Però hi ha altres que admeten més girs. Per això hem de trobar un centre de gir (al centre de la pròpia figura) i un angle que permeti aplicar el gir invariant. Aquest "molinet" admet, a més de la volta completa, 4 posicions més que la deixen "tal qual". Per obtenir les 5 posicions de la volta completa hem de girar la figura en angles que van de 72º en 72º (72º, 144º, 216º, 288º i 360º).

Una altra possibilitat a estudiar seran les simetries. Cap de les dues figures anterior en presenta però aquesta té un eix de simetria que també la deixa invariant.

Com és lògic, aquesta figura també presenta el gir trivial de 360º.

La següent figura és més complexa. Admet 4 girs invariants en una volta completa, un cada 90º.

Però també té 4 eixos de simetria que, com pots observar, es creuen en el mateix punt que el centre gir.

 
Els Grups de Leonardo
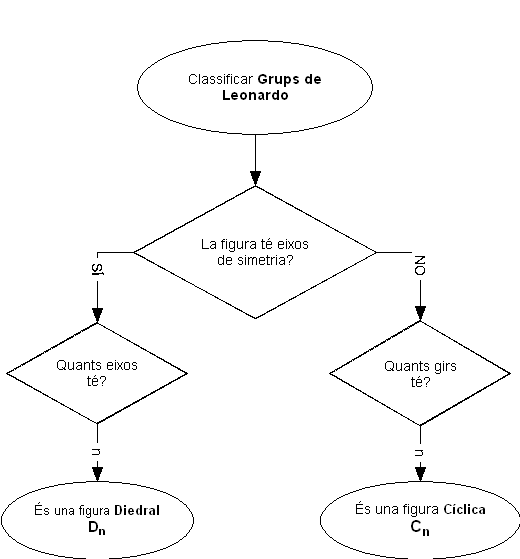
Leonardo da Vinci va classificar aquest tipus de figures en dos grans grups:
  • Cíclics: no tenen eixos de simetria. Els podem simbolitzar amb la lletra C.
  • Diedrals: tenen eixos de simetria. Els podem simbolitzar amb la D.

Qualsevol figura es pot classificar en un d'aquests dos grups. L'única cosa que haurem d'afegir serà un subíndex que ens indiqui o bé quants girs tenim que deixin la figura invariant  en una volta completa, o bé quants eixos de simetria.

Observa a quin grup pertany cadascuna de les quatre figures anteriors:

Cíclic 1 (C1) Diedral 1 (D1)
C5 D4

I un cercle que serà? Un grup diedral infinit?

La resposta és que no. Per classificar en un Grup de Leonardo una figura ha de tenir un nombre finit d'eixos o de girs.