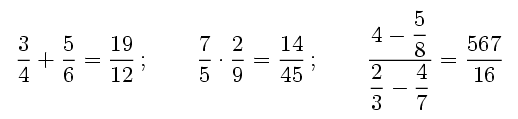| |
|
|
| |
En aquesta pràctica i la següent es tracta de
fer servir tot el que ja hauràs après fins ara (i potser
una mica més) per tal d'elaborar alguna cosa prou complexa: un
projecte amb tots els ets i uts!
|
|
| |
|
|
| |
Aritmètica
de fraccions de nombres enters |
|
| |
|
|
| |
Et proposem, doncs, la construcció d'un conjunt de classes i mètodes
que tinguin com a finalitat l'automatització del càlcul
amb fraccions de nombres enters: allò que, en la majoria de calculadores
habituals a les aules de secundària, no pots fer si no és
que dónes els resultats com a nombres decimals:
|
|
| |
|
|
| |
|
|
| |
|
|
| |
El projecte serà,
doncs, un conjunt de classes (amb els seus mètodes, constructors,...)
que automatitzarà els càlculs amb fraccions i et permetrà
trobar els resultats en forma de fracció simplificada. |
|
| |
 |
|
| |
|
|
| |
|
|
| |
Obre el
 .
Tria l'opció de menú Projecte|Nou Projecte i comença,
doncs, per crear un projecte que convé que guardis en la carpeta
de treball (en les pràctiques anteriors t'hem aconsellat ../Bluej/projectes).
Dona a aquest projecte el nom d'Aritmetica
i, entre aquesta pràctica i la següent, l'ompliràs
amb les classes que ha de contenir. Veuràs que el programa ja t'ha
preparat la infrastructura pel teu projecte però que encara no hi
tens cap classe. |
|
| |
|
|
| |
Una classe
plena de mètodes: NombresEnters
|
|
| |
|
|
| |
La primera classe que necessites serà, només,
una mena de contenidor de mètodes per treballar amb nombres enters,
més enllà de les quatre operacions bàsiques, i no
la instanciarem mai (podríem fer-ho, però no en treuríem
cap avantatge). Serà com una mena de "biblioteca de mètodes"
que podrem cridar des d'altres classes quan ens convingui. En conseqüència,
els mètodes d'aquesta classe han d'estar disponibles sense que
se n'hagi creat cap objecte!
- Perquè això sigui així, els mètodes els
declararem com a static.
Això fa que una classe amb mètodes static
sigui quelcom més que un simple esquema, que un simple esquelet,
perque ja conté elements que són funcionals!
|
|
| |
|
|
 |
- Un mètode static vol dir, exactament,
que ja està disponible a la classe, no està lligat amb
els objectes d'aquesta classe
- Per cridar un mètode static des d'una
altra classe, cal posar com a prefix del nom del mètode el nom
de la classe que el conté:
| La_meva_classe.el_meu_metode(<...
paràmetres...>); |
i aquesta serà la manera bàsica com farem servir els mètodes
static, com ja anireu veient en el transcurs
d'aquestes pràctiques.
|
|
| |
|
|
 |
Ara, doncs, en l'entorn del
clica a Nova Classe, deixa l'opció per
defecte per crear una classe i li poses el nom NombresEnters.
Aquesta classe serà la que es tracta de fer i ha de tenir aquest
codi:
|
|
| |
|
|
| |
|
/**
* La classe NombresEnters conté alguns mètodes
static de càlcul amb
* nombres enters.
*
* @author Carles Romero
* @version 2004/01/26
*/
public class NombresEnters {
/**
* El valor absolut d'un nombre enter.
* @param a un nombre enter
* @return el valor absolut del nombre
a
*/
public static int valorAbsolut
(int a) {
int valor=a;
if
(valor<0) {
//
si a és negatiu, canviar-li el signe
valor=-valor;
}
return valor;
}
/**
* El màxim comú divisor
positiu de dos enters.
* @param a b dos nombres enters
* @return el màxim comú
divisor positiu de a i b
*/
public static int Mcd
(int a,int b) {
int divisor=valorAbsolut(a);
int residu=valorAbsolut(b);
while
(residu!=0) {
int
dividend=divisor;
divisor=residu;
residu=dividend%divisor;
}
return divisor;
}
/**
* El mínim comú múltiple
positiu de dos enters.
* @param a b dos nombres enters
* @return el mínim comú
múltiple positiu de a i b
*/
public static int Mcm (int a,int b) {
return valorAbsolut(a*b/Mcd(a,b));
}
}
|
|
|
| |
|
|
| |
Per escriure aquest codi a la teva classe NombresEnters
has de fer doble clic a la caixa que el programa li ha preparat (o botó
dret i Obrir Editor). Llavors has de modificar les propostes inicials
que et fa el programa i incloure-hi el text precedent amb el benentès
que...
- ja saps quines són les línies de comentaris; no seria
imprescindible escriure-les però t'aconsellem que ho facis per
fer més entenedora la lectura posterior del codi.
- també pots fer retallar i enganxar. Seleccionar i retallar
d'aquesta pàgina web i enganxar a la finestra d'editor del codi
del
Quan ja ho hagis fet és l'hora d'analitzar el codi amb una explicació
dels mètodes que conté la classe.
|
|
| |
|
|
| |
Valor Absolut |
|
|
| |
|
|
|
| |
El primer mètode,
public static int valorAbsolut (int a), no necessita
cap explicació especial: si el nombre a
és negatiu se li canvia el signe i, si no, se'l deixa tal com està. |
|
| |
|
|
| |
Màxim comú
divisor |
|
|
| |
|
|
| |
El segon mètode, public static int Mcd (int
a,int b), calcula el màxim comú divisor de dos nombres
mitjançant l'ús de l'algorisme d'Euclides. Molt breument:
del fet que, si a
i b són
dos nombres enters i r
és el residu de la divisió de a
entre b, aleshores
m.c.d.(a, b)
= m.c.d.(b, r), i del fet que, en una divisió
de nombres no negatius, el residu és sempre més petit que
el divisor, simplement es tracta d'anar fent les divisions successives
fins arribar a residu zero.
Aquest procediment assegura que, per trobar el màxim comú
divisor de dos nombres enters, podem dividir l'un per l'altre; tot seguit
el que era dividend passa a divisor i el residu obtingut passa a dividend
i fem la nova divisió. Si repetim aquesta acció fins que
el residu sigui 0, en aquest moment el darrer divisor emprat és
el màxim comú divisor.
El mètode comença tot assegurant que els càlculs
es faran amb nombres positius i els guarda a les variables divisor
i residu.
|
|
| |
|
|
| |
public
static int Mcd (int a,int b) {
int divisor=valorAbsolut(a);
int residu=valorAbsolut(b); |
|
|
| |
|
|
| |
Després
comença una estructura while(...){...},
que és el primer exemple de bucle
(en anglès: "loop") que apareix en aquest curs.
D'acord amb el fet que while vol dir mentre l'estructura condicional
funciona així: |
|
| |
|
|
| |
|
while (<condició>)
{ // La condició pot ser certa
o falsa
... codi ...
... codi ...
// Aquest codi s'executa només
si la
... codi ...
// condició és certa
... codi ...
}
//
Ara es torna a la primera línia de l'estructura
//
while(...){...} i es torna a examinar
//
si la condició és certa o falsa...
... més codi ... //
quan la condició ja és falsa, el programa
... més codi ... //
continua...
... més codi ...
|
|
|
| |
|
|
| |
- Mentre la condició sigui certa, s'executará una
i altra vegada el codi contingut entre les claus delimitadores {
}. Quan la condició ja sigui falsa,
se sortirà del bucle i es continuarà amb el codi que vingui
a continuació.
- Si la condició no és certa inicialment el programa no
executa cap vegada les instruccions del bucle i passa a les sentències
indicades ... més codi...
- Si, després de l'anàlisi de l'exemple que et proposem,
t'interessa veure altres exemples que poden portar-se a la pràctica
amb un bucle de programació, mira aquí.
Vegem ara l'exemple que ens ocupa. El nostre bucle repeteix el cicle
(les sentències del cos del bucle, que més
avall examinarem) mentre residu
sigui diferent de zero. Adoneu-vos de quin és per a Java
el signe que permet comprovar si els valors de dues variables son diferents:
és !=
|
|
| |
|
|
| |
|
|
| |
Dels dos nombres, cal
guardar el primer que era divisor, en una altra
variable intermèdia int dividend:
|
|
| |
|
|
| |
|
|
| |
Tot seguit es fa que
el segon dels nombres, que havíem designat com a residu,
passi a ser el divisor: |
|
| |
|
|
| |
|
|
| |
i calcula el nou residu
amb l'operador mòdul, %.
(a%b dóna el
residu de la divisió entera de a
per b) : |
|
| |
|
|
| |
|
|
| |
Quan residu
sigui zero, divisor (on hi tenim el darrer divisor
emprat) ja serà el màxim comú divisor: |
|
| |
|
|
| |
|
|
| |
Mínim comú
múltiple |
|
|
| |
|
|
| |
- El tercer mètode, public static int Mcm
(int a,int b), aprofita el fet que, si a
i b són
dos nombres enters, aleshores
a·b = mcd(a,b)·mcm(a,b)
|
|
| |
| return
valorAbsolut(a*b/Mcd(a,b)); |
|
|
| |
|
|
| |
Funcionament dels
mètodes |
|
|
| |
|
|
| |
Ara hem d'anar per verificar el funcionament d'aquests mètodes.
Compila la classe NombresEnters. Recorda que
ho pots fer des de l'entorn del ,
botó dret del ratolí sobre la caixa de la classe i Compilar,
o bé des de l'editor de codi desant primer els canvis i clicant
a Compilar.
Sense crear cap objecte de la classe, comprova què fan
aquests mètodes, cosa que et mostrem amb unes imatges.
|
|
| |
|
|
| |
- public static int valorAbsolut (int a):
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
- public static int Mcd (int a,int b):
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
- public static int Mcm (int a,int b):
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
 |
Mètodes
recursius: |
|
| |
|
|
| |
El mètode
public static int Mcd (int a,int b) pel càlcul
del màxim comú divisor dels nombres a
i b es pot escriure d'una manera força
més elegant que la d'abans: |
|
| |
|
|
|
|
/**
* El màxim comú divisor
positiu de dos enters.
* Versió recursiva.
* @param a b dos nombres enters
* @return el màxim comú
divisor positiu de a i b
*/
public static int Mcd (int a,int b) {
if
(b==0) { // el segon nombre és
zero?
return
valorAbsolut(a);
//
Sí: el Mcd és el 1r nombre
}
else {
return
Mcd(b,a%b);
// b no és 0: calcula el Mcd del segon i
//
del residu del 1r entre el 2n
}
}
|
|
|
| |
|
|
| |
Com que m.c.d.(a,
0) = a, les línies de codi |
|
| |
|
|
| |
if
(b==0) { // el segon nombre és
zero?
return
valorAbsolut(a);
//
Sí: el Mcd és el 1r nombre |
|
|
| |
|
|
| |
es justifiquen per
elles mateixes. D'altra banda, com que, si r
és el residu de la divisió de a
entre b, aleshores
m.c.d.(a, b) =
m.c.d.(b, r), i l'operació a%b
dóna, precisament, el residu de la divisió de a
entre b, les línies |
|
| |
|
|
| |
}
else {
return
Mcd(b,a%b);
//
b no és 0: calcula el Mcd del segon i
// del residu del 1r entre el 2n
}
|
|
|
| |
|
|
| |
queden perfectament
explicades. Finalment, com que cada residu a%b
és, cada vegada, estrictament menor que l'anterior, és clar
que, en algun moment, el càlcul arribarà a a%b==0
i el mètode acabarà. |
|
| |
|
|
|
Observa que, en aquest
mètode, la línia |
|
| |
|
|
| |
fa una crida a ell
mateix. Els mètodes que fan això es diuen mètodes
recursius i solen ser més eficients que els que fan la
mateixa feina, però no són recursius. |
|
| |
|
|
|
Pràctica,
pràctica! |
|
| |
|
|
| |
Un
primer exercici per a comprovar les teves habilitats en mètodes recursius
és aquest: |
|
| |
|
|
| |
 Escriu
un mètode recursiu,
public
static int potencia (int a,int n),
que retorni a elevat a la potència
n, és a dir, a
multiplicat n vegades per sí mateix.
Has d'aprofitar els fets que a0
= 1, i que an
= a·an-1. Naturalment,
el mètode entraria en un cicle infinit si n
< 0. Això se soluciona amb un objecte Exception,
però no t'ho expliquem fins a la propera pràctica.
|
|
| |
|
|
| |
Si no te'n surts (ep!
només si no te'n surts), o bé, vols comparar el teu
codi amb el que nosaltres proposem, trobaràs la solució d'aquest
exercici aquí.
|
|
| |
|
|
| |
Encara
un altre exercici. Escriu un mètode recursiu,
public static int factorial(int
n),
que retorni el factorial n!
del nombre n,
això és:
n! = n·(n - 1)·(n - 2)·...·3·2·1.
Per exemple, 3! = 3·2·1
= 6 i 5! = 5·4·3·2·1
= 120.
Per definició, 0!
= 1 i n! =
n·((n - 1)!).
|
|
| |
|
|
| |
La solució és
aquí. |
|
| |
|
|
| |
Comentari final: |
|
|
| |
|
|
| |
Tot
i que, com ja t'hem comentat, els mètodes recursius solen ser els
més potents, en aquests dos exercicis que acabem de plantejar hi
ha una característica que sovint hom demana als programes informàtics:
la repetició d'un procediment (multiplicar a
per sí mateix un munt de vegades; multiplicar uns nombres, el resultat
per l'anterior, etc...).
- En aquesta pràctica has vist un procediment del tipus bucle
(while) que t'ofereix una altra manera d'enfocar
els dos mètodes anteriors. A veure si te'n surts! També
(ep! només si no te'n surts) pots consultar el codi de
la potència
i el factorial
amb un while.
- Ara bé, també és interessant que sàpigues
que, més endavant, t'explicarem un altre procediment d'iteració
|
