ACTIVITAT 5.10
EL TEOREMA DE PITÀGORAS RETROBAT

Menú inicial
Activitat anterior

Menú de la unitat 5

Si en l'activitat anterior hem demostrat un teorema de Tales utilitzant productes escalars, en aquesta demostrarem el teorema de Pitàgoras, en forma directa i en forma inversa, també utilitzant productes escalars.

Teorema de Pitàgoras en forma directa:

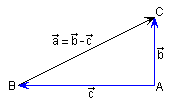Sigui un triangle ABC rectangle en A, i siguin = i =, és a dir, els catets (veure la figura). Aleshores podem posar la hipotenusa com la diferència = -; calculem el seu mòdul al quadrat:
                ||² = |-|² = (-)² =² - 2·+² =²+² = ||²+ ||²
ja que al ser el dos vectors i perpendiculars, el seu producte escalar és zero. Obtenim doncs que el quadrat de la hipotenusa és la suma dels quadrats dels catets.

Teorema de Pitàgoras en forma inversa:
Sigui un triangle ABC que verifica  ||² = ||²+ ||² , (essent =, = i ==-). Aleshores, com que sempre es verifica
               ||² = |-|² = (-)² =² - 2·+² = ||² - 2·+ ||²
ha de ser necessàriament  2·, per tant ·= 0, els dos vectors i són perpendiculars, i el triangle ABC és rectangle amb angle recte en A.

ACTIVITAT INTERACTIVA

Aquest applet mostra que si dos vectors i són perpendiculars (és a dir, ·= 0) aleshores entre ||, || i |-| es verifica la relació:
         |-|² = ||²+ ||²
(que anomenarem relació de Pitàgoras) i recíprocament.

Quines de les següents parelles de vectors i verifiquen la relació de Pitàgoras |-|² = ||²+ ||² ?

1)=(2,5) i =(7,-3)
2)=(-2,5) i =(10,4)
3)=(2,4) i =(6,-2)
4)=(6,9) i =(3,-2)

SOLUCIÓ