APLICACIÓ DE LA INTEGRACIÓ AL CÀLCUL D'ÀREES

4. APLICACIÓ DE LA INTEGRACIÓ AL CÀLCUL D'ÀREES

Recordem que el valor de la integral I :

depèn del signe de la funció f(x) en [a,b], per tant si volem calcular l'àrea tenim que considerar els següents casos:

4.1 Àrea d'un trapezi mixtilini determinat per una funció definida positiva en [a,b]:

El valor de la integral I és positiu, perquè f(x) ho es en l'interval [a,b]:

Per tant el valor de l'àrea del trapezi mixtilini coincideix amb el valor d'I :

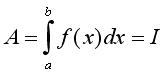
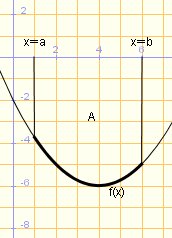
4.2 Àrea d'un trapezi mixtilini determinat per una funció definida negativa en [a,b]:

En aquest cas com f(x) és negativa la integral també ho serà:

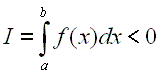
Per tant per calcular l'àrea hem de fer el valor absolut d'I:

4.3 Àrea d'un trapezi mixtilini determinat per una funció que talla l'eix de les abscisses en [a,b]:

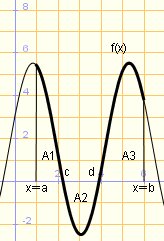
En aquest cas I pot prendre qualsevol valor positiu, negatiu o zero.

Per calcular l'àrea hem de conèixer primer en quins valors s'anul·la la funció, i després calcular l'àrea en cada fragment de diferent signe (com en els casos anteriors) L'àrea total es pot calcular com a suma de A1, A2, A3:

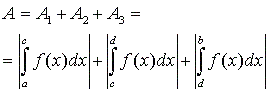
Observem que el primer i tercer valor absolut no es necessari en aquest cas.

PRACTICA 4.1.

Obre la finestra de la Wiris i observa les diferencies entre I i A, definides com en els apartats anteriors.

EXERCICI 4.1

Calculeu l'àrea trapezis mixtilinis limitats per les funcions, l'eix d'abscisses i els valors a i b que s'indiquen en cada cas:

a) entre a=2 i b=4

b) entre a=-2 i b=1

c) entre

d) entre a=0 i b=3

Ajuda

Solució


pàg ant	inici	pàg seg