|
L'altre dia quan vam veure els límits d'una funció quan `x->\infty` vam acabar començan a parlar d'una cosa desconcertant. Resulta que podiem parlar de límit quan `x` tendia a un número. Que no és res més que veure cap on s'acosten les imatges d'una funció, `f(x)` a mesura que les, `x`, s'acosten a un cert número. En general n'hi podem dir, `a`. Segurament tothom deu pensar, quina pregunta més tonta, cap on vols que s'acostin les imatges si no a la imatge, `f(a)`?. Per exemple si tenim la funció, `f(x)=x^2` i us pregunteu cap on s'acosten les imatges si `x` s'acosta (tendeix) a 3. Tots tindreu claríssimament clar que s'acosten a `9`, ja que, `f(3)=3^2=9`. Però la vida és molt dura i això només passarà si les funcions són contínues i no sempre la realitat és com ens agradaria que fos. Penseu que, en molts casos, ni tan sols està definida la funció en el punt al qual volem saber el límit, per exemple si us demano quan val el `lim_{x\to 3}1/(x-3)`, segur que tots us adoneu que no podem trobar el límit buscant la imatge degut a que la `f(x)=1/(x-3)` no té imatge en el `3`, ja que tenim una divisió per `0`. Després de tot aquest rotllo que la majoria, pot ser, no hi ha entès res, ho explicarem amb exemples. Més tard podeu tornar a llegir això i veureu com tot comença a tenir sentit. Comencem amb la funció de l'apartat anterior. La gràfica de la qual és:  Ens hi acostarem i vurem quan val el `lim_{x\to 1}(3x^3)/(2x^2-5x)`  I ningú tindrà cap dubte que: Però què passa si busquem quan val `lim_{x\to 0}(3x^3)/(2x^2-5x)`. Si busquem la imatge, `f(0)=(30^3)/(2·0^2-5·0)=0/0`. O sigui no té imatge, per la qual cosa per trobar el límit que cerquem no ho podem fer així. Per entendre què passa i quan val el límit farem una cosa a la gràfica, li treurem els eixos i ho veurem més clar.  Veiem que en el lloc on hi hauria d'haver la imatge hi ha un forat. De fet ja a quart quan passava això ja li havíem posat un nom. Deiem que en `x=0`, hi ha una discontinuïtat de forat. Si sabem omplir el forat per treure la discontinuïtat, el valor que hem de posar a `f(0)` serà el límit buscat. En el nostre cas si mireu la gràfica tots tindreu clar que el valor que hauria de tenir `f(0)=0`. Per la qual cosa direm que: Però com sempre, la vida és molt dura i no sempre tindrem accés al dibuix de la gràfica per saber quan valen els límits. O sigui la pregunta següent és: Si ens donen una funció i ens demanen un límit de la funció quan `x` tendeix a un nombre i al substituir no ens dona cap valor, com es fa per trobar el límit? O anirem veient amb uns quants exemples. Afegir que si la funció està definida a trossos la cosa es complica un xic en el sentit de què és diferent, no és que sigui més difícil, però això per més endavant. En un cas com la funció que acabem de veure el que s'ha de fer és descomposar els polinomis i simplificar. En aquest cas és molt senzill ja que només cal trure factor comú. `lim_{x\to 0}(3x^3)/(2x^2-5x)=lim_{x\to 0}(3x^3)/(x·(2x-5))=lim_{x\to 0}(3x^2)/(2x-5)=(3·0^2)/(2·0-5)=0/(-5)=0` Abans de veure altres exemples semblant anem-nos a preguntar quan val, `lim_{x\to 2'5}(3x^3)/(2x^2-5x)` Si representem la gràfica:  I veiem clàrament que `lim_{x\to 2'5}(3x^3)/(2x^2-5x)=\infty`. Analíticament també es veu, ja que si substituïm: `lim_{x\to 2'5}(3·2'5^3)/(2·2'5^2-5·2'5)=(46'875)/0=\infty`. Ja que si dividim una cosa que tendeix a un número per una cosa cada vegada més a prop del `0` tot plegat se'n va cap a `\infty`. Per saber si és a `+` o a `-` una forma de fer-ho és buscar la imatge d'un `x` a l'esquerra del `2'5`, per exemple, `2'4`. `f(2'4)=(3·2'4^3)/(2·2'4^2-5·2'4)=-86'4`, que com és negatiu voldrà dir que: Això és llegeix, límit quan `x` tendeix a `2'5` per l'esquerra, s'indica així, `2'5^-`. Per buscar el límit per la dreta del `2'5`, cal buscar la imatge d'un `x` a la dreta, per exemple, `2'6`. `f(2'4)=(3·2'6^3)/(2·2'6^2-5·2'6)=+101'4`, que com és positiu voldrà dir que: Això és llegeix, límit quan `x` tendeix a `2'5` per la dreta, s'indica així, `2'5^+`. A continuació farem uns quants exemples. Calcularem uns quants límits: En principi substituïm sempre. `lim_{x\to 1}(x^2-4)/(x^2+x-6)=(1^2-4)/(1^2+1-6)=3/4` Si dona un número aquest és el límit. Per la qual cosa el que hem de fer és descomposar els polinomis i simplificar. `lim_{x\to 2}(x^2-4)/(x^2+x-6)=lim_{x\to 2}((x-2)·(x+2))/((x+2)·(x+3))=lim_{x\to 2}(x+2)/(x+3)=4/5` Ara mirarem si va cap a `+\infty` o a `-\infty`. Calcularem els límits laterals. Per fer-ho aprofitarem la feina feta abans, la descomposició i trobarem el signe d'una manera més científica que la que hem fet abans. `lim_{x\to -3^-}(x^2-4)/(x^2+x-6)=lim_{x\to -3^-}((x-2)·(x+2))/((x+2)·(x+3))=lim_{x\to -3^-}(x+2)/(x+3)=-1/-=+\infty` Ja que a l'esquerra del `-3` és números són`-3'1` i `-3'1+3=-` `lim_{x\to -3^+}(x^2-4)/(x^2+x-6)=lim_{x\to -3^+}((x-2)·(x+2))/((x+2)·(x+3))=lim_{x\to -3^+}(x+2)/(x+3)=-1/+=-\infty` Ja que a la dreta del `-3` és números són`-2'9` i `-2'9+3=+` Si dibuixem la gràfica veurem que tot això és compleix.  1-`lim_{x\to 1}(x^3-x^2+x+2)/(2x^2-2x+2)=(1^3-1^2+1+2)/(2·1^2-2·1+2)=3/2` 2-`lim_{x\to 1}(x^3-2x^2-x+2)/(x^3+x^2-2x)=0/0` Per la qual cosa cal descomposar. Fem Ruffini i surt. Recordeu que els dos polinomis són divisibles per `(x-1)` ja que `1` és una arrel de tots dos: `lim_{x\to 1}(x^3-2x^2-x+2)/(x^3+x^2-2x)=lim_{x\to 1}((x-1)·(x^2-x-2))/((x-1)·(x^2+2x))=lim_{x\to 1}(x^2-x-2)/(x^2+2x)=(-2)/3` Donada la funció, 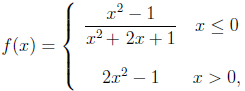 Calculeu. `lim_{x\to -1}f(x)`, `lim_{x\to 0}f(x)`, `lim_{x\to 2}f(x)`
Calculem els límits per la dreta i l'esquerra. `lim_{x\to -1}((x-1)·(x+1))/((x+1)^2)=lim_{x\to -1}(x-1)/(x+1)=(-2)/0=\infty` `lim_{x\to -1^-}((x-1)·(x+1))/((x+1)^2)=lim_{x\to -1^-}(x-1)/(x+1)=(-2)/(-1'1+1)=(-/-)=+\infty` `lim_{x\to -1^+}((x-1)·(x+1))/((x+1)^2)=lim_{x\to -1^+}(x-1)/(x+1)=(-2)/(-0'9+1)=-/+=-\infty`
`lim_{x\to 0^+}f(x)=lim_{x\to 0^+}2x^2-1=-1` Com que els dos límits són iguals podem dir sense cap problema que: `lim_{x\to 0}f(x)=-1`
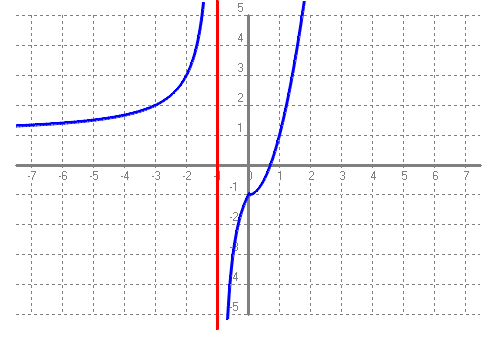 A continuació el que cal és fer exercicis al respecte: |