 |
- Euclides,
Arquímedes y Apoloni de Perga, van ser les
tres grands figures matemàtiques de l'helenisme.
- Euclides representa la sistematizació del saber
matemàtic,
- Arquímedes, va ser l'autèntic geni polifacètic,
i
- Apoloni, el menys conegut, fou des del punt de vista
matemàtic l'autèntic especialista en geometria.
El seu treball, Les Còniques, no es va conèixer
al món occidental fins l'any 1710, quan va ser publicat
per Edmond Halley. Pel
que fa a la seva vida, en sabem molt poques coses: Nascut cap
a la meitat del segle III a C a Perga, sembla ser que va
viure molt de temps a Alexandria, on la Biblioteca constituia
en aquell temps el centre del saber occidental.
|
|
- Apoloni
supera extraordinàriament tots els coneixements sobre còniques
(el·lipse, hipèrbola,
paràbola) que fins llavors es tenien i a més els
presenta d'una forma molt millor organitzada. Els seus coneixements
i descobriments sobre còniques els va escriure en una obra,
Les Còniques, que consta de vuit volums, dels quals
els quatre primers només són una introducció
elemental i sembla que recullen tot allò que, probablement,
se sabia fins llavors sobre les còniques; en aquests quatre
primers llibres s'exposen: modes d'obtenir les còniques
i propietats bàsiques, diàmetres, eixos i asímptotes,
teoremes notables, propietats dels focus i intersecció
de dos còniques.
- En el llibre
I defineix les còniques com a resultat de seccionar amb
un plan un con circular de dues fulles (figura 1). En aquest mateix
llibre considera també el centre, els eixos, diàmetres
conjugats, tangents, etc. i ataca fins i tot el problema de construir
una cònica a partir de diversos elements seus.
|
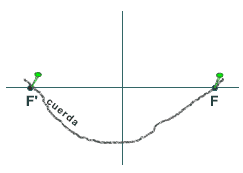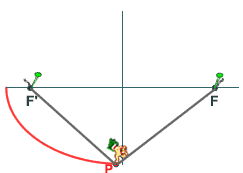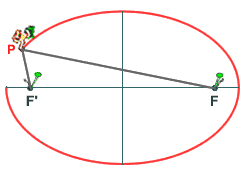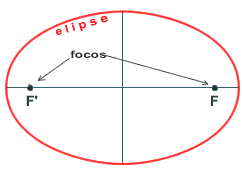
Figura 2
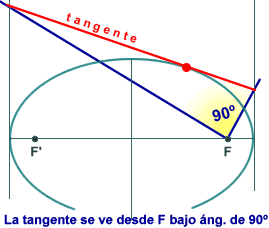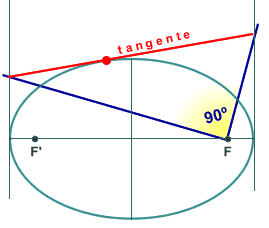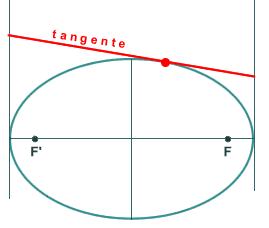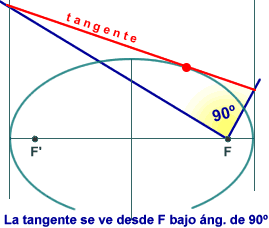 Figura 3
Figura 3
|
- En el llibre
II estudia fonamentalment les propietats de les asímptotes
de la hipèrbola. Al final, tracta també el següent
problema: Traçar una tangent que formi un angle donat
amb el diàmetre que passa pel punt de contacte.
- En el llibre
III, un dels de més valor, apareix ja el que avui prenem
normalment com a definició d'el·lipse, és
a dir, l'el·lipse és el
þ lloc
geomètric dels punts tales que la suma de les seves distàncies
a dos punts fixos, F y F', és constant (figura
2).
En aquest mateix llibre se estudien també les relacions
de triangles i quadrilàters determinats per tangents i
diàmetres conjugats, apareix també la hipèrbola
com a lloc dels punts tales que el producte de les seves distàncies
a dues rectes fixes és constant, i hi apareixen interessants
propietats sobre els focus, com ara la de la figura 3:
þ des
d'un focus F de l'el·lipse, es veu sota un angle recte
el segment de qualsevol tangent determinat per les tangents en
els vèrtexs.
- Pel que fa
al llibre IV, en ell estudia el nombre de punts d'intersecció
de les còniques; conté 55 proposicions i és
de destacar el fet que les 23 primeres apareguin fetes pel mètode
de reducció a l'absurd.
|
|
Els resultats
que s'exposen en els llibres V, VI i VII són descobriments
del propi Apoloni i es refereixen a:
- Segments
de màxima i mínima distància a les còniques,
normal, centre de corbatura (llibre V, considerat el millor
i el més original, en el qual introdueix ja, a la seva
manera, conceptes tales com el de normal a una corba, evoluta,
centre de corbatura, etc,.. i obté ja aquests elements
per a les còniques de la manera més rigorosa).
- Igualtat
i semblança de les seccions còniques (llibre
VI, en el qual resol molt elegantment el següent problema:
donats una cònica i un con circular recte, determinar una
secció del con que sigui igual a la cònica.).
- Relacions
mètriques sobre diàmetres conjugats, àrees,
etc. (llibre
VII).
Finalment, sobre
el llibre VIII, es desconeix encara el contingut.
|

 |
|
|

