
|
- Sense
dubte, Arquímedes fou la figura màxima de la matemàtica
grega i un dels més grans científic-matemàtics de
tots els temps. Nascut a Siracusa (Sicília) l'any
287 aC, es va educar a Alexandria (Egipte), però
aviat va tornar a la seva ciutat natal, on va fer un intens treball
científic fins que va morir. Al final de la seva vida va
participar en la defensa de Siracusa contra els romans,
construint armes de guerra (catapultes, sistemes de miralls per
incendiar naus,...) amb les quals es va aconseguir endarrerir
notablement la conquesta de la ciutat. L'any 212 aC, però,
la ciutat va caure en poder de les tropes del general Marcel,
i durant el conseqüent saqueig, Arquímedes morí
travessat per l'espasa d'un soldat romà, tot i que Marcel,
segons ens conta Plutarco, havia ordenat que l'agafessin
viu i no li fessin cap mal.
|
|
-
Els treballs d'Arquímedes són autèntiques
memòries científiques, treballs originals en els que sempre
s'aporten elements nous, no coneguts fins llavors. Per fer-los,
va utilitzar rigorosament el mètode euclídeo de fixar exactament
les hipòtesis i enunciar i demostrar curosament els teoremes
subsegüents. Tota la seva obra fou escrita en varis tratats;
De l'esfera i el cilindre, Dels conoïdes i dels esfereïdes,
Quadratura de la paràbola, De la mesura del cercle i El
Sorral, són els seus principals escrits sobre matemàtiques,
encara que Arquímedes te també destacats escrits sobre
estàtica, com ara el que porta el títol De
l'equilibri dels plans, en el qual enuncia la llei d'equilibri
de la palanca, i en hidrostàtica, com el de títol
Dels cossos flotants, en el qual estudia científicament
l'equilibri dels cossos submergits i enuncia el que coneixem avui
com a principi d'Arquímedes.
Sembla ser que aquest descobriment el va fer quan es banyava,
pensant com resoldre un problema que li havia encarregat el rei
Heró de Siracusa.
|
-
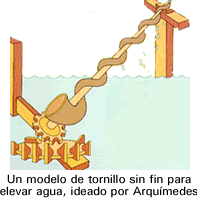
En mecànica, Arquímedes va fer nombrosos treballs;
va definir, per exemple, la llei de la palanca i es considerat
com l'inventor de la politja composta. Durant la seva estada a
Egipte, va inventar també el cargol sense fi per
a pujar l'aigua de nivell.
Arquímedes va passar la major part de la seva vida a Siracusa,
dedicat a la recerca i i als experiments. Malgrat no tenir cap
càrrec públic, durant la conquesta de Sicília per
els romans es va oferir, com ja hem dit, a les autoritats de la
ciutat i molts dels seus instruments mecànics van ser utilitzats
per defensar-la. Entre la maquinària de guerra la invenció
de la qual se li atribueix, està la catapulta
i un sistema de miralls amb els quals incendiava els vaixells
enemics enfocant-los amb els raigs del sol.
|
|
- En
el camp de las matemàtiques pures, es va avançar
a molts dels descobriments de la ciència moderna, com ara
el càlcul integral, amb els seus estudis d'àrees
i volums de figures sòlides corbades i d'àrees de
figures planes. Va demostrar, per exemple, que el volum d'una
esfera és dos terços del volum del cilindre que
la circumscriu, i va trobar i va demostrar les fórmules de
l'àrea del cercle, la de la superfície
de l'esfera, la de l'àrea tancada per un segment
de paràbola, etc. No només això, sinó
que, a més, va tenir la idea de fer servir mètodes
mecànics per a obtenir resultats matemàtics, que
després demostrava rigorosament seguint mètodes
de demostració de matemàtics anteriors tales com Euclides
o Eudoxe (mètode d'exhaució).
- A
la dreta podeu veure el mètode que va utilitzar per obtenir
aproximacions del nombre pi (passeu el ratolí
per sobre):Va construir polígons regulars inscrits i circumscrits
a una circumferència, fent així una estimació
de la longitud d'aquesta mitjançant els perímetres dels
polígons. Així, va arribar a treballar amb polígons
de fins a 96 costats i llavors va deduir que pi s'havia
de trobar necessàriament entre las fraccions 223/71 i 22/7,
és a dir, entre 3'1408... y 3'1428..
|
|
- La seva obra
mestra, però, potser sigui Sobre l'esfera i el cilindre,
en la qual determina àrees i volums d'esferes i cossos
relacionats, aconseguint així per a sòlids tridimensionals
allò que ja havia aconseguit per a figures planes en el
seu escrit Mesura del cercle. Aquesta fou al menys l'obra
que el mateix Arquímedes considerava com el seu triomf
més gran, ja que va demanar que es gravés a la seva
tomba la imatge d'una esfera i un cilindre circumscrit, amb la
inscripció Vcil = 1'5 Vesf.
- També es
va interessar Arquímedes per qüestions aritmètiques,
com ho demostra la seva obra El Sorral, amb la qual pretén
provar que el nombre de grans de sorra que omplís tot l'univers
es podria comptar i, fins i tot, numerar. L'interès d'aquesta
obra és doble: Per una banda, crea un sistema de numeració
propi per a treballar amb grans nombres, i d'altra banda, és
l'únic escrit en el que demostra tenir bons coneixements astronòmics,
donant fins i tot un mètode per calcular el diàmetre
aparent del Sol.
|
|
|
 Ý
Ý
|
|
Sobre
qualsevol cos submergit en un líquid actua una força
cap amunt (empenyment) el valor de la
qual és igual al pes del líquid que ha desallotjat
(figura a la dreta).
|
|
| |
Llegenda
associada al principi d'Arquímedes.
Diuen que
el rei Heró de Siracusa havia lliurat a un joier una certa quantitat
d'or perquè amb ella li fes una corona. Quan ja estava
acabada, la gent deia que el joier havia substituït una
part de l'or per una quantitat equivalent de plata, devaluant
així la corona i, per la qual cosa, enganyant al rei.
Llavors, aquest va demanar Arquímedes que descobrís si
veritablement havia estat enganyat. Arquímedes, capficat
en el problema, va descobir un dia la solució mentre es banyava
i llavors, saltant del bany, va córrer totalment nu pels
carrers de Siracusa cridant: ¡eureka! ¡eureka!. Ell havia
descobert que, pesant el volum d'aigua desplaçat per
la corona en submergir-la, podia esbrinar si contenia la mateixa
quantitat d'or que el rei havia donat al joier. |
|

|
|
Imaginem
una línia trencada ABC (segment AC doblat en un punt B). El
seu punt mig, M, es pot determinar mitjançant el següent
mètode:
- Es
fa l'arc de circumferència que passa pels tres punts
A, B y C.
- Es
calcula el punt mig, M', de l'arc de circumferència
AC.
- Llavors,
la perpendicular a BC traçada por M' dóna
sobre BC el punt mig, M, de la corda doplegada ABC.
|
|
| Curiosament,
utilitzant aquest teorema, es pot deduir la fórmula trigonomètrica
sen(x-y) = senx·cosy - cosx·seny |
|

|
|
Quan hom diu que un vaixell
desplaça 20 tones, podem saber el pes total del vaixell?.
Quant val l'empenyment experimentat pel vaixell cap amunt
mentre navega?
|
|
|
|

