| Hi
ha tres nombres irracionals les aplicacions dels quals, tant a matemàtiques
com a altres disciplines, són tan nombroses i importants que
podríem dir de tots tres que són els irracionals
més famosos. Són els nombres p
(pi), e, f
(fi), anomenats
nombre pi, nombre e y nombre
d'or, respectivament. Dos d'ells, p
i f, ja eren coneguts pels
grecs, varis segles abans de Crist; el nombre e és
àmpliament utilitzat des del segle XVIII. |

|
- Des d'antiguitats
molt remotes se sap que en totes les circumferències
la relació entre la seva longitud y el seu diàmetre
dóna sempre el mateix resultat; aquest resultat s'ha
vingut designant amb la lletra grega p,
que és la inicial de la paraula grega perifèria
(periferia). El valor de p
ha estat una preocupació constant entre els matemàtics
des del segle III abans de Crist; durant molts segles es va pensar
que p era igual a alguna fracció
de dos enters i va haver molts intents per trobar-la, però
només es van obtenir aproximacions notables, tales com
- p
= 22/7 = 3,1428... (Arquimedes, segle III aC.)
- p
= 377/120 = 3,14166..., (Ptolomeo, segle II dC.)
- p
= 355/113 = 3,141592.., (Tsu Ch'ung-Chi, segle V, dC)
Potser el
cas més sorprenent sigui el de l'anglès William
Shanks, qui va dedicar 20 anys de la seva vida a l'obtenció
de xifres decimals de p.
A finals del segle XIX, va donar els 707 primers decimals de
p, però, en 1945,
es va descobrir que havia comès un error al decimal 528,
i a partir d'aquest els altres eren incorrectes.
|
|
- En 1767 el
matemàtic Johann Lambert va demostrar que p
no es podia expressar com a fracció, és a dir, que
p era irracional, per
la qual cosa tots els esforços es van centrar ja en aconseguir
fórmules cada vegada millors per aconseguir bones aproximacions
de p. De fet, algunes fórmules
ja havien sigut obtingudes abans de demostrar la irracionalitat
de p,
tales com
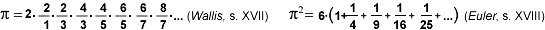
- Tot nombre
obtingut després de un nombre finit de passos a partir
d'enters, usant només amb ells les operacions suma,
resta, multiplicació, divisió i radicació,
s'anomena nombre algebraic (Dit d'altra manera,
els nombres algebraics són aquells que són
solució d'alguna equació polinòmica de quoficients
enters.). Euler, en el segle XVII, va anomenar transcendents
als nombres que no eren algebraics, és a dir, transcendents
perquè transcendeixen més enllà de les operacions
habituals de l'àlgebra. Fins al segle XIX no es va
conèixer el primer nombre transcendent, i va ser
a finals del mateix segle, en 1882, quan Lindemann va demostrar
que p es transcendent.
- El descobriment
de Lindemann va permetre resoldre de pas un dels tres
problemes clàssics de l'antiguitat, el de la quadratura
del cercle; en ser p transcendent,
la quadratura del cercle era impossible.
- p
apareix en moltes qüestions que no tenen res a veure amb
circumferències. Per exemple,
- Imagina
que agafem a l'azar dos nombres en la sèrie natural
(1, 2, 3, 4, ...). Imagines quàntes possibilitats tenim
de què els nombres agafats no tinguin cap factor comú?
La resposta es sorprenent (i difícil de trobar): En
el 6/p% = 1,91% dels casos
haurem agafat dos nombres primos entre sí (o sigui,
sense cap factor comú).
- Imagina
que agafem a l'azar dos nombres decimals positius menors que
1. Te imagines quant val la probabilitat que els dos nombres
junt amb el nombre 1 pueguin ser els costats d'un triangule
obtusangle?. La resposta torna a ser sorprenent: És
(p-2)/4=0'2878, o sigui
serà possible en el 28'78% dels casos.
- Una anècdota
curiosa sobre el nombre p.
- Va succeir
l'any 1897 a Indiana, EE.UU., i el protagonista fou un metge
de nom Goodwin, qui va creure que havia realitzat un descobriment
sobre la relació entre el cercle i la circumferència,
cosa que implicava un impressionant resultat sobre p.
Va portar el cas al terreny polític demanant al seu representant
a la Assemblea General d'Indiana que presentés com a
proposició de Llei local el següent text: "L'Assemblea
General de l'estat d'Indiana decreta que se ha descobert que
l'àrea del cercle és igual al quadrat que té
el costat de longitud igual al quadrant de la circumferència".
És immediat deduir d'això que p=4.
La proposició es va presentar i va passar a la aprovació
d'un primer comitè, posant-se així en marxa un
procediment per a ser aprovada pel ple del Senat, amb la qual
cosa hauria adquirit el rang de llei. Afortunadament per "als
pares de les lleis", va ser retirada en l'últim
moment, cosa que va evitar caure en un ridícul que hauria
adquirit el rang d'històric.
- Veure
més sobre el nombre p
|

|
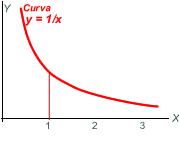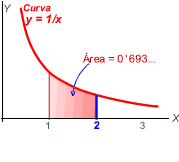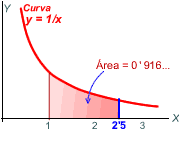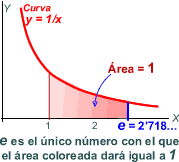
El
nombre e, i la seva eterna companya la funció logaritme
neperià, tenen nombroses aplicacions a totes les branques
de la ciència, l'economia, etc. Abans d'indicar-ne algunes,
vegem 3 definicions, diferents però equivalents, d'aquest nombre
(també irracional i transcendent, com el p),
el valor del qual és, aproximadament, 2'718,,,
|
|
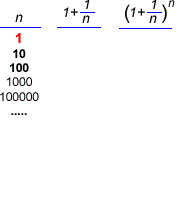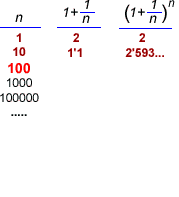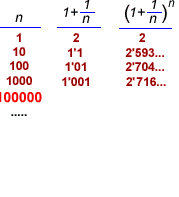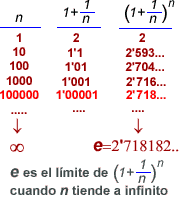
Definició
1
|
Definició
2
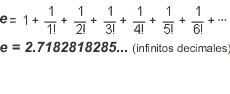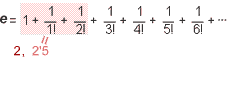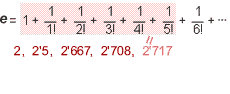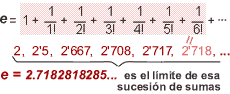
|
Definició
3
|
|
Alguns exemples d'aplicació
- T'has
preguntat alguna vegada quina és la forma més rentable
de cobrar l'interès ofert per un Banc?
- Si invertim
un capital a un interès compost anyal del 10% (tema
del que tothom sembla que en sap), la fórmula que
estableix quant recollirem després de n anys és
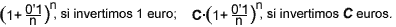
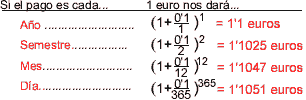
- Ara bé,
potser fora millor si ens paguessin cada 6 mesos a raó
del 5%? Seria encara millor si ens paguessin cada mes a raó
de l' 1%? Potser millor que ens el paguessin diàriament
al 10/365% =0' 0274%? Si pensem en quant recolliríem en
un sol any, posant 1 euro, veiem que
- Ja posats,
per què no imaginar que ens donen l'interès per
hores, o per minuts, o per segons, o...fins
i tot de manera continua!? No podria ser aquesta la millor
de les formes possibles? El cert és que sí, que
és la forma que ens donaria el millor rendiment possible
per a un 10% anyal. Aquest rendiment, per a 1 euro seria, lògicament,
el valor límit de l'expressió
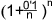 quan n tendeix a l'infinit, el qual resulta ser
quan n tendeix a l'infinit, el qual resulta ser 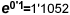 . .
- Aquest creixement
continu al qual ens acabem de referir no té res d'estrany
al món animal. Els models proposats pels economistes,
biòlegs, etc per a estudiar creixements de poblacions
solen basar-se en la idea anterior, i acaben en fórmules
que, inevitablement, inclouen potències del nombre e
amb la variable temps a l'exponent.
- T'has
dit alguna vegada com van arribar els científics a una
fórmula per esbrinar l'edat d'un esquelet, un fòssil,
etc? Saps que també el coneixement del nombre e
va ser fonamental?
- Cap a
la meitat del segle XX, el químic Libby va descobrir
el carboni-14, un isòtop radioactiu del carboni
que desapareix lentament (la
seva vida mitjana és de 5568 anys, és
a dir, una quantitat donada de C14 triga 5568 anys a reduir-se
a la meitat). El C14 reacciona amb l'oxigen a les capes
altes de la atmosfera donant diòxid de carboni radioactiu,
el qual entra a la superfície de la Terra, en la qual
es desenvolupa la vida. Libby deia: Com que les
plantes viuen del diòxid de carboni, tindran totes
alguna quantitat de radioactivitat, i el mateix succeirà
amb els animals terrestres, ja que viuen d'elles. Mentre
un ésser sigui viu, anirà reposant el C14 que
perdi, però quan l'ésser és mort, només
es produirà en ell una pèrdua contínua
i lenta de C14.
- Una vegada
que els químics van aconseguir arribar a mesurar la
quantitat de C14 continguda en un ésser no viu, com
que es coneixia la velocitat de desintegració del C14,
es podia pensar en arribar a una equació que els hi
donés com a solució el temps necessari
per a que en aquest ésser quedés només
aquesta quantitat de C14, suposant raonablement que en els
animals i plantes vius del passat existien quantitats similars
a les d'ara. Tan sols quedava, doncs, trobar una fórmula
que involucrés la quantitat inicial (CI)
de radioactivitat, la quantitat actual (CA)
i el temps (t). Doncs bé, la fórmula
trobada va ser:
(A
la fórmula, Ln2 = 0'69315 és el nombre al que
s'ha d'elevar e per a obtenir un resultat igual a 2)
|
 |
- El nombre
f, o nombre d'or,
es una de las dos soluciones de la equació X
² = 1-X.
Concretamente,
|
|
La otra solución
es, precisamente, 1/f =
1,618...
- El nombre
f aparece
en campos tan variados como los reinos vegetal y animal, la poesía,
la música, la arquitectura, el arte, etc. y se designa
con la letra griega "fi" en honor de Fidias,
considerado el escultor de las obras más perfectas de la
antigua Grecia.
-
Desde
hace cinco segles, el rectángulo considerado como "el
más bello" es aquel en el cual la relación
entre la altura y la anchura da resultat igual
a f.
-
El
rectángulo "más bello" tiene la propiedad
de que al quitarle el cuadrado más grande posible, o
sea, el de lado igual al lado menor, resulta otro rectángulo
más pequeño que también es de "máxima
belleza" (Fíjate en la igura 2)
-
Así,
podriamos continuar el proceso de división con
este rectángulo menor e iríamos obteniendo rectángulos
cada vez más pequeños, los cuales serían
siempre de "máxima belleza". Luego, uniendo
los extremos de esos cuadrados obtendríamos la llamada
espiral áurea, presente en objetos naturales
tales como la concha del Nautilus, la distribución
de semillas del girasol, el feto humano, etc. (figura 3,
Nautilus)
- Según
las tradiciones que proponen un canon de belleza del cuerpo humano,
si tomamos 1 como medida total del cuerpo, entonces la medida
de los pies al ombligo debe ser exactamente f.
(figura 4, ideal de L. da Vinci)
- Leonardo
de Pisa, apodado Fibonacci, planteó en el segle
XIII un problema sobre reproducción de conejos que daba
como resultat la sucesión
1, 1,
2, 3, 5, 8, 13, 21, ....,
Dicha sucesión
tiene importabans en Ciencias de la Naturaleza y cada término
de ella se obtiene sumando los dos anteriores a él. Curiosamente,
si vas dividiendo cada término por su siguiente en la
sucesión, verás que salen aproximaciones cada
vez mejores del nombre d'or. Eso no es extrany,
ya que en realidad el límite de tales divisiones es el
nombre d'or.
Veure
més sobre el nombre d'or |
 
|
|
|
|
El hombre de Vitubrio
Para
Leonardo da Vinci, las dimensiones a y b en
el cuerpo perfecto deben dar un cociente igual a 0'618....
|
|
A LA DIVINA PROPORCIÓN
A
ti, maravillosa disciplina,
media,
extrema razón de la hermosura,
que claramente acata la clausura
viva en la malla de tu ley divina.
A
ti, cárcel
feliz de la retina,
áurea
sección, celeste cuadratura,
misteriosa fontana de mesura
que el universo armónico origina.
A ti, mar de los sueños angulares,
flor
de las cinco formas regulares,
dodecaedro azul, arco sonoro.
Luces por alas un compás ardiente.
Tu canto es una esfera transparente.
A ti, divina
proporción d'or.
R.
Alberti
|
|

|
|

