 |
- Cap
a l'any 600 aC va viure el gran Tales de Milet, qui és
considerat generalment com el primer matemàtic demostratiu
conegut. La següent figura important de les matemàtiques
a la Grècia antiga fou Pitàgores, nascut
a Samos l'any 572 aC.
- Pitàgores
va viure a la part sud de l'actual Itàlia, a la
ciutat grega de Crotona, i allà va crear una societat
secreta d'estudis que coneixem avui amb el nom d'escola pitagòrica.
Els pitagòrics vivien en comunes i es regien per unes normes
extraordinàriament estrictes, fins al punt que, segons
es diu, tenien prohibida la ingestió de certs aliments (per exemple,
la carn, les mongetes, ...), i la divulgació dels seus descobriments
els hi podia costar fins i tot la vida; ells van difondre la doctrina
de Pitàgores, de qui no es conserva cap escrit (potser
per això, alguns han arribar fins i tot a dubtar de la
seva exsitència)
- Van
destacar a música, astronomia i, sobre tot, a matemàtiques.
En la seva contemplació del món, consideraven el nombre
enter com l'essència de totes les coses: "tot es
nombre", era el seu lema. Per sobre de qualsevol altra
aportació, s'han de destacar dues: el famós enunciat
conegut com a "teorema de
Pitàgores" i el descobriment de les quantitats
irracionals, és a dir, quantitats que no podien ser mesurades
mitjançant cap nombre enter ni trencat; concretament, van
descobrir que la diagonal i el costat de un quadrat
no podien ser mesurats a la vegada, i exactament, usant una unitat
de mesura comú; van decidir expressar aquest fet dient que ambdues
longituds són incommensurables (no mesurables amb
una unitat comú). Això els hi va suposar un autèntic
maldecap, no només perquè feien servir la idea de
la commensurabilitat de segments en les seves demostracions geomètriques,
sinó perquè, a més, feia caure tota la seva
teoria filosòfica sobre el paper central del "nombre
enter"; diu la llegenda que, enfadats per la pertorbació
que els hi produïa, van abandonar mar endins Hippaso,
el seu descobridor.
- Pel
que fa al famós teorema, se sap que més de 1000
anys abans els babilonis ja el coneixien; la primera demostració,
però, es atribuïda unànimement als pitagòrics.
Diu la llegenda que Pitàgores va ordenar que se sacrifiqués
un bou als deus per a celebrar el descobriment de la demostració.
Aquí us donem 3 demostracions gràfiques diferents del esmentat
teorema; l'última va ser feta per Gardfield,
el vigèsim president dels Estats Units d'Amèrica.
La primera de les tres ja l'haureu vista a la pàgina de
presentació.
|
| |
 Ý
Ý
|
|
| |
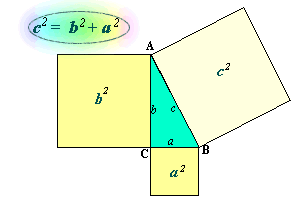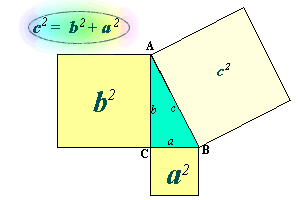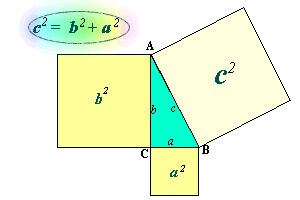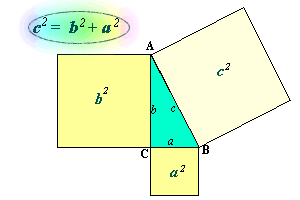
En
qualsevol triangle rectangle, ABC, el quadrat del costat més
gran (hipotenusa) dóna el mateix que
la suma dels quadrats dels costats petits (catets).
És a dir, el quadrat construït sobre la hipotenusa dóna
la mateixa superfície que la suma dels quadrats construïts
sobre els catets.
NOTA.Els
escolàstics
consideraven el teorema de Pitàgores com la frontera entre
la geometria accesible per a tothom i la geometria innaccesible
per a la majoria; per això, li deien el "pont dels burros"
|
|
|
| |
|
|
| |
Demostració
2

|
Demostració
3
(Garfield,
20º president dels EEUU.)

|
|

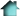
|
|
|
|

