Segons
la definició de producte escalar, que és  · · =| =| || || |cos( |cos( ^ ^ ),
si tenim dos vectors ),
si tenim dos vectors  i
i  no nuls i perpendiculars,
el seu producte escalar és zero (ja que formen un angle de
90º i cos90º = 0). no nuls i perpendiculars,
el seu producte escalar és zero (ja que formen un angle de
90º i cos90º = 0).
Recíprocament, si el producte
escalar de dos vectors no nuls  i
i  és zero,
el cosinus de l'angle que formen ha de ser zero (ja que no són
zero ni | és zero,
el cosinus de l'angle que formen ha de ser zero (ja que no són
zero ni | | ni
| | ni
| |), l'angle que
formen és de 90º, i els vectors són perpendiculars. |), l'angle que
formen és de 90º, i els vectors són perpendiculars.
Aquest fet ens permet donar la
següent definició:
Dos vectors són
perpendiculars (u ortogonals)
si
el seu producte escalar és zero
Simbòlicament, si indiquem la perpendicularitat amb
^:  ^ ^ Û Û
 · · = 0
= 0
És interessant observar
dues coses:
1) Recordant com es calcula el producte escalar a partir dels
components, la condició de perpendicularitat de dos vectors
donats pels seus components és
 =
(a1,a2) ^ =
(a1,a2) ^  =
(b1,b2) Û =
(b1,b2) Û
 · · = a1b1+ a2b2 = 0
= a1b1+ a2b2 = 0
2) Hem estès la definició de perpendicularitat també
a vectors nuls, i segons aquesta nova definició, el vector
nul és perpendicular a qualsevol altre vector.
|
|
|
ACTIVITAT INTERACTIVA
1) Utilitzant
 · · =
(a1,a2)·(b1,b2)
= a1b1+ a2b2 digues
quins dels següents parells de vectors tenen producte escalar
zero i, per tant, són perpendiculars. Comprova-ho a l'applet
de la dreta. =
(a1,a2)·(b1,b2)
= a1b1+ a2b2 digues
quins dels següents parells de vectors tenen producte escalar
zero i, per tant, són perpendiculars. Comprova-ho a l'applet
de la dreta.
|
a) (4,1)
i (1,4)
|
b) (4,1)
i (-1,4)
|
|
c) (-1,2)
i (4,2)
|
d) (3,2)
i (1,-3)
|
|
e) (6,2)
i (-1,3)
|
f) (5,2)
i (0,0)
|
|
g) (3,2)
i (-3,-2)
|
h) (6,-3)
i (2,-1)
|
|
i) (2,1)
i (4,5)
|
j) (3,0)
i (0,-2)
|
2) Dibuixa el vector  =
(-2,3) i tracta de dibuixar dos vectors perpendiculars a =
(-2,3) i tracta de dibuixar dos vectors perpendiculars a  .
Quins són els seus components? .
Quins són els seus components?
SOLUCIÓ
|
|
1) Obté dos
vectors perpendiculars a cadascun dels vectors:
 =
(5,6) =
(5,6) |
 =
(-7,4) =
(-7,4) |
 =
(-3,-1) =
(-3,-1) |
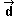 =
(0,-3) =
(0,-3) |
2) Obté dos vectors perpendiculars
al vector = (4,3) que tinguin
mòdul 10. = (4,3) que tinguin
mòdul 10.
|
