Les funcions definides a trosso es caracteritzen per estar formades per trossos d'altres gràfiques, i acostuma a tenir punts de discontinuïtat o punxes, la fórmula té l'aspecte següent:

Obre el programa FUNCIONS I GRÀFIQUES, clica sobre la icona . Apareixerà una nova finestra on podràs introduir les diferents fórmules i els intervals corresponents. Observa que pots introduir fins a cinc funcions definides a trossos diferents (FT1(x),...FT5(x)) i cadascuna pot està formada per set expressions.

Anem a representar la funció :

Introdueix les expressions i els nombres tal i com pots veure a la imatge següent:

Clica D'acord i obtindràs la gràfica següent.

Clica sobre la icona . Selecciona FT2(x) . Introdueix les expressions i els nombres necessaris per representar la gràfica de la funció.

Modifica l'expressió 2 x de la fórmula anterior perquè el resultat sigui una funció contínua.

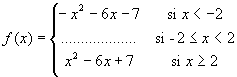
Troba els valors de la variable independent que fan que la imatge sigui més petita que 0,5 en la funció anterior.

La Calculadora WIRIS també ens permet representar gràfiques de funcions definides a trossos. Per definir la funció tenim diverses alternatives, la que utilitzarem la pots observar en l'exemple següent:

Quina és la fórmula de la funció anterior?

Representa gràficament la funció:

Accedeix a la pestanya Edició i clica sobre la icona . Aleshores apareixerà una nova finestra, clica Aceptar . Seguidament, apareixerà una finestra amb la calculadora WIRIS i amb la vora de color negre, en comptes del blau. Al menú Archivo d'aquesta nova finestra de l'explorador, tria Guardar Como... i desa'l amb el nom func_def_trossos.htm .

Utilitza qualsevol dels dos programes per esbrinar la fórmula de les dues funcions de finides a trossos que s'han creat a partir de h (x) = x+2, i(x) = - x+2, j(x) = - x² i k(x) = x² -1.