 |
Les funcions de proporcionalitat inversa
es caracteritzen per tenir una fórmula del tipus f(x)
=  , la gràfica
és una hipèrbola i a la taula de valors podem observar
que el producte x·y és constant i coincideix
amb el valor d'a , la gràfica
és una hipèrbola i a la taula de valors podem observar
que el producte x·y és constant i coincideix
amb el valor d'a
|
 |
Obre el programa FUNCIONS I GRÀFIQUES,
activa l'opció ESBORRAR EN REPRESENTAR NOVA FUNCIÓ
del menú VISUALITZAR. Representa la gràfica de la
funció
f(x) = 1/x.
Ara, introdueix l'expressió següent: f(x)
=  .
Mou la barra de desplaçament corresponent al paràmetre
u i respon les preguntes següents: .
Mou la barra de desplaçament corresponent al paràmetre
u i respon les preguntes següents:
|
 |
Quina és la fórmula
de la funció la gràfica de la qual passa pel punt
(6 , 2)?
Quina relació hi ha entre el nombre a i la gràfica
de la funció f(x) =  ?
Què passa si el coeficient de a és negatiu? ?
Què passa si el coeficient de a és negatiu?
|
 |
Clica sobre les icones  i
i  .
Representa gràficament la funció f(x)
= .
Representa gràficament la funció f(x)
=  . Activa
l'opció del menú VISUALITZAR | VISUALITZAR COORDENADES
CURSOR (X,F(X)), Observa que a la part superior esquerra apareixen
les coordenades dels punts de la gràfica i sobre la gràfica
apareix senyalat el punt corresponent. Omple la taula següent
a partir de la gràfica: . Activa
l'opció del menú VISUALITZAR | VISUALITZAR COORDENADES
CURSOR (X,F(X)), Observa que a la part superior esquerra apareixen
les coordenades dels punts de la gràfica i sobre la gràfica
apareix senyalat el punt corresponent. Omple la taula següent
a partir de la gràfica:
Tria un punt qualssevol de
la gràfica (x , y) comprova que x ·
y = 12 . Investiga com, en casos semblants amb aquest, podem
esbrinar la fórmula de la funció.
|
 |
Quin ha estat el resultat de la teva investigació?
|
 |
Clica sobre les icones  i
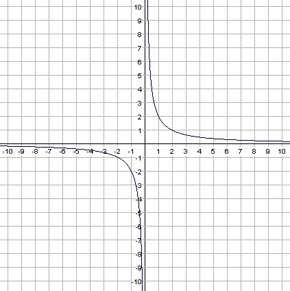
i  per esborrar les gràfiques i les fórmules. Esbrina
la fórmula de les funcions que tenen les gràfiques
següents i comprova-ho fent la representació gràfica:
per esborrar les gràfiques i les fórmules. Esbrina
la fórmula de les funcions que tenen les gràfiques
següents i comprova-ho fent la representació gràfica:
 |
|
|
f(x)=
|
f(x)=
|
|
 |
Crea amb la calculadora WIRIS un seguit
d'instruccions que permetin trobar la fórmula i fer la representació
gràfica d'una funció de proporcionalitat inversa que
passi per un punt determinat. Fes-ho de forma semblant a com ho
vas fer a l'activitat dedicada a la funció afí. Desa'l
amb el nom func_prop_inversa.htm.
|
